Algorithm Complexity
Computer science is a scientific field that relies heavily on the study of algorithms. To measure an algorithm's efficiency, we need criteria to compare it. This section discusses how to analyze an algorithm from a scientific perspective.
Suppose M is an algorithm and n is the input data size. The time and space used by the algorithm M are two primary measures of its efficiency. The time is measured in key operations--in sorting algorithms, for example, it would be the number of comparisons. This is because key operations are so defined that other operations' time will be significantly less. On the other hand, space is determined by counting the maximum amount of memory needed by the algorithm.
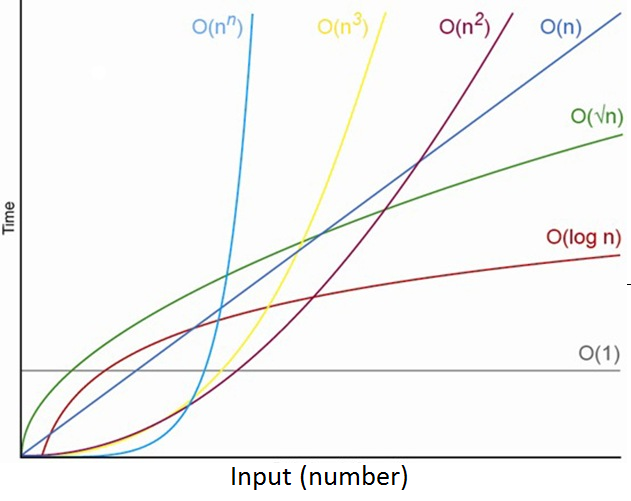
The complexity of an algorithm M is the function f(n), which is the number of operations completed for a given time duration or in relation to the size of the data input. Unless otherwise stated or implied, complexity refers to the computation's run time.
Let's take a look at an example of how the function f(n), which gives the running time of an algorithm, may change.
Suppose we are given an English short story called STORY, and suppose we want to search through STORY for the first occurrence of a given 3-letter word WORD. If WORD is the 3-letter word “the,” then it is likely that WORD occurs near the beginning of STORY, so f(n) will be small. On the other hand, if WORD is the 3- letter word “zoo,” then WORD may not appear in STORY at all, so f(n) will be significant.
The above discussion leads us to find some complexity function f(n) instances.
Worst case: the maximum value of f(n) for any possible input
Average case: the expected value of f(n)
Best case: the minimum possible value of f(n)
