Bridge Edge of a Graph
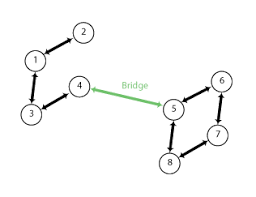
Exploring Graph Algorithms : Bridge Edge of a Graph
The quest to identify bridge edges in a graph is a captivating challenge that invites us to navigate the intricate landscape of graph algorithms. By unraveling the connections between nodes and leveraging algorithmic tools like Tarjan's Algorithm, we not only find crucial structural elements but also enhance our understanding of graph theory. As we traverse the graph landscape, we discover the power and elegance of algorithms in solving real-world problems and maintaining the integrity of interconnected networks.
Introduction to Graph Algorithms
The realm of graph algorithms presents an equally captivating and practical playground for honing your algorithmic skills and exploring the intricacies of data structures. Graph algorithms unlock hidden patterns and relationships within connected networks, opening doors to diverse applications in various fields.
Imagine a world interconnected by roads, friendships, or even neurons in a brain. These connections, represented as edges, bridge nodes (think cities, people, or neurons) in a complex web called a graph. Graph algorithms equip us with tools to navigate and analyze these intricate relationships, revealing hidden insights and solving real-world problems. Traversing a graph involves visiting nodes and following edges. But instead of linear sequences, we explore branching paths, encounter cycles, and grapple with interconnectedness. Algorithms like Depth-First Search (DFS) and Breadth-First Search (BFS) become our trusty guides
Bridge Edge of a Graph
Bridging the gap between connected components in a graph lies a special set of edges – the bridges. These sentinels guard the connectivity of the graph, and their removal leads to its fragmentation. But how do we identify these crucial guardians? Here's a procedure to unveil them:
- Depth-First Search (DFS): A classic explorer, DFS delves deep into the graph, marking nodes with "discovery times" – the order they're visited. When an edge leads to a node already visited with an earlier time, it's not a bridge – another path connects them. But if the edge leads to a future-time node, it's a bridge, holding the fort against disconnection!
- Trajan's Algorithm: This advanced knight utilizes a similar "discovery time" concept but adds a "low-link" value – the minimum discovery time reachable from a node (including itself) through back edges. If an edge's low-link surpasses its destination's discovery time, it's a bridge, standing strong against the threat of disconnection.
With your chosen algorithm and a dash of exploration, you've identified the bridge edges, the guardians of your graph's connectivity. Now, use them to analyze network robustness, optimize communication flow, or unlock other hidden insights within the web of connections.
Python Code
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = defaultdict(list)
def add_edge(self, u, v):
# Add an undirected edge between vertices u and v
self.graph[u].append(v)
self.graph[v].append(u)
def find_bridges(self):
bridges = []
def bridge_util(current, visited, parent, low, disc):
nonlocal bridges
visited[current] = True
disc[current] = low[current] = self.time
self.time += 1
for neighbor in self.graph[current]:
if not visited[neighbor]:
# Recur for the unvisited neighbor
parent[neighbor] = current
bridge_util(neighbor, visited, parent, low, disc)
# Update low value
low[current] = min(low[current], low[neighbor])
# Check for a bridge
if low[neighbor] > disc[current]:
bridges.append((current, neighbor))
elif neighbor != parent[current]:
# Update low value for the visited neighbor
low[current] = min(low[current], disc[neighbor])
# Initialize data structures
visited = [False] * self.V
parent = [-1] * self.V
low = [float('inf')] * self.V
disc = [float('inf')] * self.V
self.time = 0
# Call the bridge utility function for each unvisited vertex
for vertex in range(self.V):
if not visited[vertex]:
bridge_util(vertex, visited, parent, low, disc)
return bridges
# Example usage:
g1 = Graph(5)
g1.add_edge(1, 0)
g1.add_edge(0, 2)
g1.add_edge(2, 1)
g1.add_edge(0, 3)
g1.add_edge(3, 4)
print("Bridges in the graph:")
bridges = g1.find_bridges()
for bridge in bridges:
print(bridge)
Step-by-Step Explanation
1. Importing Libraries
from collections import defaultdict
This line imports the defaultdict class from the collections module. defaultdict is a subclass of the built-in dict class and overrides one method to provide a default value for a nonexistent key.
2. Class Definition: Graph
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = defaultdict(list)
Graphis a class that represents an undirected graph.- The
__init__method initializes the graph with a given number of vertices (vertices). It also creates a defaultdict to store the graph, where each vertex is associated with a list of its neighbors.
3. Method: add_edge
def add_edge(self, u, v):
# Add an undirected edge between vertices u and v
self.graph[u].append(v)
self.graph[v].append(u)
add_edgeis a method to add an undirected edge between two verticesuandv. It appendsvto the list of neighbors ofuand vice versa.
4. Method: find_bridges
def find_bridges(self):
bridges = []
def bridge_util(current, visited, parent, low, disc):
nonlocal bridges
visited[current] = True
disc[current] = low[current] = self.time
self.time += 1
for neighbor in self.graph[current]:
if not visited[neighbor]:
# Recur for the unvisited neighbor
parent[neighbor] = current
bridge_util(neighbor, visited, parent, low, disc)
# Update low value
low[current] = min(low[current], low[neighbor])
# Check for a bridge
if low[neighbor] > disc[current]:
bridges.append((current, neighbor))
elif neighbor != parent[current]:
# Update low value for the visited neighbor
low[current] = min(low[current], disc[neighbor])
find_bridgesis a method that finds all bridges in the graph using a helper functionbridge_util.bridge_utilis a nested function that performs a Depth-First Search (DFS) traversal to find bridges. It keeps track of visited vertices, discovery times (disc), and low values.- Bridges are identified based on the conditions specified in the code.
5. Example Usage
- An instance of the
Graphclass (g1) is created with 5 vertices. - Edges are added to the graph.
- The
find_bridgesmethod is called to identify and print the bridges in the graph.
C++ Code
#include <bits/stdc++.h>
using namespace std;
class Graph
{
int V; // Number of vertices
list<int> *adj; // Adjacency list to represent the graph
// Utility function to find bridges using DFS traversal
void bridgeUtil(int u, vector<bool> &visited, vector<int> &disc,
vector<int> &low, int parent);
public:
Graph(int V); // Constructor
void addEdge(int v, int w); // Add an edge to the graph
void bridge(); // Find and print all bridges
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v); // Graph is undirected
}
void Graph::bridgeUtil(int u, vector<bool> &visited, vector<int> &disc,
vector<int> &low, int parent)
{
static int time = 0; // Static variable for simplicity
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
// Explore all neighbors of the current node
for (int v : adj[u])
{
if (v == parent) // Skip the edge to the parent
continue;
if (visited[v])
{
// If v is already visited, update the low value of u
low[u] = min(low[u], disc[v]);
}
else
{
// Recur for the unvisited neighbor
parent = u;
bridgeUtil(v, visited, disc, low, parent);
// Update the low value of u
low[u] = min(low[u], low[v]);
// Check for a bridge
if (low[v] > disc[u])
cout << u << " " << v << endl;
}
}
}
void Graph::bridge()
{
vector<bool> visited(V, false);
vector<int> disc(V, -1);
vector<int> low(V, -1);
int parent = -1; // No parent for the initial call
// Call the recursive helper function for each unvisited vertex
for (int i = 0; i < V; ++i)
{
if (!visited[i])
{
bridgeUtil(i, visited, disc, low, parent);
}
}
}
int main()
{
cout << "\nBridges in the graph\n";
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
return 0;
}
Step-by-Step Explanation
1. Header and Namespace
#include <bits/stdc++.h>
using namespace std;
This includes the necessary headers for standard C++ library components.
#include <bits/stdc++.h> is a commonly used include statement that includes most standard headers.
2. Class Definition: Graph
class Graph
{
int V;
list<int> *adj;
Defines a class named Graph to represent an undirected graph.
V: Number of vertices in the graph.
adj: Pointer to an array of lists, each list represents the adjacency list of a vertex.
3. Constructor: Graph(int V)
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
This initializes a graph with a given number of vertices.
V is set to the given number of vertices.
Dynamic memory is allocated for the adjacency list.
4. Method: addEdge(int v, int w)
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v);
}
Adds an undirected edge between vertices v and w to the graph.
Adds w to the adjacency list of v and vice versa.
5. DFS-based Bridge Finding Utility Function: bridgeUtil
void Graph::bridgeUtil(int u, vector<bool> &visited, vector<int> &disc,
vector<int> &low, int parent)
{
static int time = 0;
This implements a DFS-based utility function to find bridges in the graph.
time: A static variable to keep track of discovery time.
6. DFS-based Bridge Finding Utility Function (Continued)
visited[u] = true;
disc[u] = low[u] = ++time;
This marks the current node as visited and initializes discovery time and low value.
7. DFS-based Bridge Finding Utility Function (Continued)
for (int v : adj[u])
{
if (v == parent)
continue;
if (visited[v])
{
low[u] = min(low[u], disc[v]);
}
else
{
parent = u;
bridgeUtil(v, visited, disc, low, parent);
low[u] = min(low[u], low[v]);
if (low[v] > disc[u])
cout << u << " " << v << endl;
}
}
}
Explores all neighbors of the current node.
Updates low values and identifies bridges based on conditions.
8. Method: bridge
void Graph::bridge()
{
vector<bool> visited(V, false);
vector<int> disc(V, -1);
vector<int> low(V, -1);
int parent = -1;
for (int i = 0; i < V; ++i)
{
if (!visited[i])
{
bridgeUtil(i, visited, disc, low, parent);
}
}
}
Initiates the bridge-finding process for the entire graph.
9. Main Function
- Creates an instance of
Graph(g1) with some vertices. - Adds edges to represent a sample graph.
- Calls the
bridgemethod to find and print bridges.
Java Code
import java.util.*;
public class bridge_edge {
private static class Graph {
private int V; // Number of vertices
private LinkedList<Integer> adj[]; // Adjacency list to represent the graph
private int time = 0;
private static final int NIL = -1;
// Constructor
@SuppressWarnings("unchecked")
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList<>();
}
// Function to add an edge into the graph
void addEdge(int v, int w) {
adj[v].add(w); // Add w to v's list.
adj[w].add(v); // Add v to w's list
}
// A recursive function that finds and prints bridges using DFS traversal
void bridgeUtil(int u, boolean visited[], int disc[], int low[], int parent[]) {
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
// Go through all vertices adjacent to this
Iterator<Integer> i = adj[u].iterator();
while (i.hasNext()) {
int v = i.next(); // v is the current adjacent of u
// If v is not visited yet, then make it a child of u in DFS tree and recur for
// it.
// If v is not visited yet, then recur for it
if (!visited[v]) {
parent[v] = u;
bridgeUtil(v, visited, disc, low, parent);
// Check if the subtree rooted with v has a connection to one of the ancestors
// of u
low[u] = Math.min(low[u], low[v]);
// If the lowest vertex reachable from the subtree under v is below u in DFS
// tree, then u-v is a bridge
if (low[v] > disc[u])
System.out.println(u + " " + v);
}
// Update the low value of u for parent function calls.
else if (v != parent[u])
low[u] = Math.min(low[u], disc[v]);
}
}
// DFS based function to find all bridges. It uses the recursive function
// bridgeUtil()
void bridge() {
// Mark all the vertices as not visited
boolean visited[] = new boolean[V];
int disc[] = new int[V];
int low[] = new int[V];
int parent[] = new int[V];
// Initialize parent and visited arrays
Arrays.fill(parent, NIL);
// Call the recursive helper function to find Bridges in DFS tree rooted with
// vertex 'i'
for (int i = 0; i < V; i++)
if (!visited[i])
bridgeUtil(i, visited, disc, low, parent);
}
}
public static void main(String args[]) {
// Create graphs given in above diagrams
System.out.println("Bridges in the graph ");
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
System.out.println();
}
}
Step-by-Step Explanation
1. Class Definition: Graph
private static class Graph {
private int V; // Number of vertices
private LinkedList<Integer> adj[]; // Adjacency list to represent the graph
private int time = 0;
private static final int NIL = -1;
// Constructor
@SuppressWarnings("unchecked")
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList<>();
}
This defines a nested static class Graph to represent an undirected graph.
private static class Graph
This defines a nested static class named Graph. It encapsulates the functionality of an undirected graph and contains:
private int V; // Number of vertices
Represents the number of vertices in the graph.
If V is 5, the graph has 5 vertices.
private LinkedList<Integer> adj[]; // Adjacency list to represent the graph
Represents the graph using an adjacency list. For each vertex, it stores a list of adjacent vertices.
adj[0] might contain [1, 2, 3] if vertices 1, 2, and 3 are adjacent to vertex 0.
private int time = 0;
Used to keep track of the discovery time during the DFS traversal.
In DFS, time is incremented as each node is visited.
private static final int NIL = -1;
A constant representing a special value indicating no parent. It's typically used to initialize parent arrays.
parent[i] = NIL; sets the parent of vertex i to an initial invalid value.
@SuppressWarnings("unchecked")
This annotation is used to suppress compiler warnings related to generic types when using arrays. In this case, it's applied to the array of linked lists.
It prevents a warning that would otherwise be generated due to the use of raw types in the array creation.
Graph(int v) { ... }
Constructor method for the Graph class. Initializes the graph with a given number of vertices.
Graph g = new Graph(5); creates a graph with 5 vertices.
adj = new LinkedList[v];
Allocates memory for the adjacency list array. Each element of the array is a linked list.
adj[2] = new LinkedList<>(); initializes an empty linked list for vertex 2.
for (int i = 0; i < v; ++i) adj[i] = new LinkedList<>();
Initializes each linked list in the array, making them empty initially.
This loop sets up an empty linked list for each vertex in the graph.
2. Method: addEdge(int v, int w)
// Function to add an edge into the graph
void addEdge(int v, int w) {
adj[v].add(w); // Add w to v's list.
adj[w].add(v); // Add v to w's list
}
Adds an undirected edge between vertices v and w to the graph and also adds w to the adjacency list of v and vice versa.
3. DFS-based Bridge Finding Utility Function: bridgeUtil
// A recursive function that finds and prints bridges using DFS traversal
void bridgeUtil(int u, boolean visited[], int disc[], int low[], int parent[]) {
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
// Go through all vertices adjacent to this
Iterator<Integer> i = adj[u].iterator();
while (i.hasNext()) {
int v = i.next(); // v is the current adjacent of u
// If v is not visited yet, then make it a child of u in DFS tree and recur for it.
// If v is not visited yet, then recur for it
if (!visited[v]) {
parent[v] = u;
bridgeUtil(v, visited, disc, low, parent);
// Check if the subtree rooted with v has a connection to one of the ancestors
// of u
low[u] = Math.min(low[u], low[v]);
// If the lowest vertex reachable from the subtree under v is below u in DFS tree,
// then u-v is a bridge
if (low[v] > disc[u])
System.out.println(u + " " + v);
}
// Update the low value of u for parent function calls.
else if (v != parent[u])
low[u] = Math.min(low[u], disc[v]);
}
}
visited[u] = true;: Marks the current node as visited.disc[u] = low[u] = ++time;: Initializes the discovery time (disc[u]) and low value (low[u]) for the current nodeu. Thetimevariable is incremented.
Traverse Adjacent Vertices
Iterator<Integer> i = adj[u].iterator();: Initializes an iterator to traverse the adjacent vertices ofustored in the adjacency list.
Recursive DFS
if (!visited[v]) { ... }: Checks if vertexvis not visited.parent[v] = u;: Setsuas the parent ofvin the DFS tree.bridgeUtil(v, visited, disc, low, parent);: Recursively callsbridgeUtilfor the unvisited vertexv.low[u] = Math.min(low[u], low[v]);: Updates the low value ofubased on the low value ofv.if (low[v] > disc[u]) System.out.println(u + " " + v);: Checks if the lowest vertex reachable from the subtree rooted atvis belowuin the DFS tree. If true,u-vis a bridge, and it's printed.
Update Low Value
else if (v != parent[u]) low[u] = Math.min(low[u], disc[v]);: Updates the low value ofufor the parent function calls. It ensures thatlow[u]considers the low value ofvfrom its children.
4. Method: bridge
// DFS based function to find all bridges. It uses the recursive function bridgeUtil()
void bridge() {
// Mark all the vertices as not visited
boolean visited[] = new boolean[V];
int disc[] = new int[V];
int low[] = new int[V];
int parent[] = new int[V];
// Initialize parent and visited arrays
Arrays.fill(parent, NIL);
// Call the recursive helper function to find Bridges in DFS tree rooted with vertex 'i'
for (int i = 0; i < V; i++)
if (!visited[i])
bridgeUtil(i, visited, disc, low, parent);
}
Initiates the bridge-finding process for the entire graph.
5. Main Function
Creates an instance of Graph (g1) with 5 vertices.
Adds edges to represent a sample graph.
Calls the bridge method to find and print bridges.
Time and Space Complexity Analysis
Time Complexity:
The time complexity of the bridge-finding algorithm is O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because the algorithm uses a depth-first search (DFS) traversal, which visits each vertex and each edge once.
In the worst case, the algorithm explores all vertices and edges in the graph. The DFS traversal takes O(V + E) time, and the additional work done to identify bridges and update the low values does not exceed this time complexity.
Space Complexity:
The space complexity of the algorithm is O(V), where V is the number of vertices. This space is used for the data structures such as arrays to keep track of visited vertices, discovery times (disc), low values (low), and parent vertices.
Specifically:
visited,disc,low, andparentarrays each use O(V) space.- The recursion depth of the DFS traversal is at most V, contributing to the call stack space.
The adjacency list representation of the graph is not considered in the space complexity analysis, as it is assumed to be given and not created by the algorithm.
Real world Applications
The bridge-finding algorithm has various real-world applications, particularly in network analysis, transportation systems, and communication networks. Here are some examples:
- Network Design and Maintenance:
- In computer networks, identifying bridges helps optimize the design and layout of the network. Bridges are critical links, and understanding them can lead to better network design and maintenance.
- Transportation Systems:
- In transportation networks, bridges can represent critical road segments or intersections. Identifying bridges helps in analyzing the robustness and efficiency of transportation systems. For instance, determining the critical road links in a city's road network can aid in traffic management and infrastructure planning.
- Communication Networks:
- In communication networks, bridges may correspond to key routers or network nodes. Identifying bridges is crucial for ensuring fault tolerance and reliability in communication systems. It helps in understanding how the removal of specific nodes may impact the overall network connectivity.
- Social Networks:
- In social network analysis, bridges could represent individuals whose connections are essential for maintaining connectivity within a community. Identifying bridges can help understand social structures and key influencers.
- Ecology and Biology:
- In ecology, bridges might represent crucial ecological corridors that facilitate the movement of species between isolated habitats. Identifying these bridges aids in conservation efforts and understanding the impact of landscape changes on biodiversity.
- Electric Power Grids:
- In power grids, bridges can represent critical transmission lines or substations. Identifying bridges is important for analyzing the vulnerability of the power grid and ensuring a reliable supply of electricity.
- Software Engineering:
- In software engineering, the concept of bridges can be applied to dependencies between software components. Identifying critical dependencies helps in understanding the impact of changes in one component on the entire system.
- Epidemiology:
- In epidemiology, bridges may represent individuals who are crucial for disease transmission between different populations. Identifying these bridges is essential for developing effective strategies to control the spread of diseases.
Understanding and identifying bridge edges provide valuable insights into the structure and vulnerabilities of various complex systems, making the algorithm applicable in a wide range of fields.
