Bubble Sort
Introduction to Bubble Sort:
Bubble Sort is a simple sorting algorithm that repeatedly steps through the list to be sorted, compares adjacent elements, and swaps them if they are in the wrong order. It doesn't use any fancy mathematics or data structures, just basic comparison and conditional logic. The pass through the list is repeated until the list is sorted. The algorithm gets its name because smaller elements "bubble" to the top of the list.
Working Principle:
- Start with the first element in the list.
- Compare it with the next element.
- If the current element is greater than the next element, swap them.
- Move to the next pair of elements and repeat steps 2-3.
- Continue this process until the end of the list is reached.
- After the first pass, the largest element is guaranteed to be at the end of the list.
- Repeat the process for the remaining elements until the entire list is sorted.
Understanding Bubble Sort through an Example:
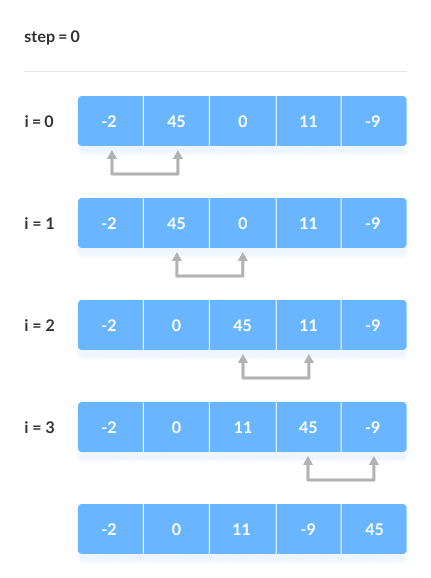
Suppose we have an unsorted array of numbers: [6, 4, 9, 3, 7]. The goal of bubble sort is to arrange these numbers in ascending order, so the final result would be [3, 4, 6, 7, 9].
Here's how bubble sort would go about sorting the array:
- First, the algorithm would compare the first two elements (6 and 4) and swap them since 4 is smaller than 6. The corrected array becomes [4, 6, 9, 3, 7].
- Next, the algorithm would compare the second and third elements (6 and 9) and no swap is necessary sinche 6<9. Array=[4,6,9,3,7]
- Then the algorithm compares third and fourth elements (9 and 3) swap them since 9 is larger than 3. The corrected array becomes [4, 6, 3, 9, 7].
- The algorithm would then compare the fourth and fifth elements (9 and 7) and swap them since 7 is smaller than 9. The corrected array becomes [4, 6, 3, 7, 9].
- Now we reached the end of the array and the largest element is sorted and placed at the last place in the list or the array.
- The algorithm repeats steps 1 to 5 for the second pass and so on until all the elements are sorted
- Array= [4,6,3,7,9]
- (4<6) - No swap needed.
- (6>3) - Swap needed. Array=[4,3,6,7,9]
- (6<7) and (7<9) no swap needed.
- Third Pass: (4>3) Swap needed. Array=[3,4,6,7,9]
- The array is sorted by this time. and it would compare all the other elements to check whether they are in sorted order to complete the third pass.
Advantages of Bubble Sort:
- Simplicity:
- Bubble Sort is one of the simplest sorting algorithms to understand and implement. This makes it an excellent educational tool for introducing the concept of sorting to beginners and students.
- In-Place Sorting:
- Bubble Sort is an in-place sorting algorithm, meaning it doesn't require additional memory space to perform the sorting. This can be advantageous in situations where memory is a critical resource.
- Adaptive:
- It is adaptive, which means that it performs well on partially sorted datasets. If a dataset is already partially sorted, Bubble Sort can have a linear time complexity in the best-case scenario.
- Stable Sorting:
- Bubble Sort is a stable sorting algorithm. Stability in sorting means that the relative order of equal elements is preserved in the sorted output. This can be important in certain applications.
- Ease of Implementation:
- The algorithm is straightforward to implement, and the logic is easy to understand. It consists of a few basic steps, making it accessible for teaching purposes and for situations where a simple sorting algorithm is sufficient.
- Small Dataset Sorting:
- For very small datasets or datasets that are nearly sorted, the overhead of more complex algorithms may outweigh the benefits. In such cases, the simplicity of Bubble Sort might make it a reasonable choice.
Disadvantages of Bubble Sort:
- Inefficiency for Large Datasets:
- Bubble Sort has a worst-case and average-case time complexity of O(n^2), making it highly inefficient for sorting large datasets. As the size of the dataset increases, the number of comparisons and swaps grows quadratically.
- Lack of Adaptability:
- The algorithm doesn't adapt well to the existing order of elements. Even if the array is partially sorted, Bubble Sort performs the same number of comparisons and swaps as it would for a completely unsorted array.
- Poor Performance on Reverse-Ordered Data:
- In its basic form, Bubble Sort performs poorly on datasets that are in reverse order. In such cases, it requires a large number of passes to bring the largest element to the correct position.
- Unstable Sorting:
- While being stable can be an advantage in certain situations, Bubble Sort's stability comes at the cost of additional comparisons. This can make it less efficient compared to other stable sorting algorithms.
- Redundant Passes:
- Bubble Sort continues to make passes through the entire list, even if the list is already sorted. This leads to unnecessary iterations and makes the algorithm less efficient.
- Not Suitable for Real-Time Applications:
- Due to its quadratic time complexity, Bubble Sort is generally not suitable for real-time applications where quick responses are required.
- Limited Use in Professional Software Development:
- In professional software development, where efficiency is crucial, Bubble Sort is rarely used for sorting large datasets. More advanced sorting algorithms like QuickSort or MergeSort are preferred.
- Comparisons and Swaps Overhead:
- The algorithm involves a significant number of comparisons and swaps, even for small datasets. This overhead becomes impractical for larger datasets and is less efficient than more sophisticated algorithms.
Real Scenarios of Bubble Sort:
- Educational Purposes:
- Bubble Sort is often used as an introductory algorithm to teach students the fundamental concepts of sorting algorithms. Its simplicity makes it an excellent starting point for beginners to understand the basic principles of sorting.
- Small Datasets:
- In situations where the dataset is small and efficiency is not a critical factor, Bubble Sort can be employed. The overhead associated with more complex algorithms might outweigh the benefits in such cases.
- Partially Sorted Data:
- If the data is already partially sorted or nearly sorted, Bubble Sort can perform reasonably well in practice. Its adaptive nature in these scenarios can make it a suitable choice.
- Embedded Systems with Limited Resources:
- In environments with limited computational resources, such as certain embedded systems, Bubble Sort might be chosen due to its simplicity and low memory requirements.
- Sorting Nearly Sorted Lists:
- When dealing with lists that are almost sorted, Bubble Sort can require fewer swaps compared to more sophisticated algorithms. In scenarios where minimizing swaps is crucial, Bubble Sort might be considered.
- In Situations with Strict Memory Constraints:
- If the memory is a significant constraint and in-place sorting is required, Bubble Sort can be a suitable choice as it doesn't require additional memory space.
- Toy or Prototype Applications:
- Bubble Sort may be used in situations where a quick-and-dirty solution is needed for a small-scale or temporary application, and the simplicity of the algorithm is more advantageous than its inefficiency.
Python code for Bubble Sort:
# Copyrights to venkys.io
# For more programs visit venkys.io
# Python program for Bubble sort
# Stable: Yes
# Inplace: Yes
# Adaptive: No
# Time Complexity: Best case - O(n), Average and worst case - O(n^2)
# Space Complexity: O(1)
# Function to perform Bubble Sort on given array
'''
Parameters:
- array (list): The list to be sorted.
Returns:
- list: The sorted list.
'''
def bubbleSort(array):
n = len(array)
# Traverse through all elements
for i in range(n):
# Last i elements are already sorted, so we don't check them
for j in range(0, n - i - 1):
# Compare adjacent elements, Swap if the elements found is greater than the next element
if array[j] > array[j + 1]:
array[j], array[j + 1] = array[j + 1], array[j]
# The sorted array is returned
return array
def main():
try:
# Taking input from the user
array = list(map(int, input("Enter the array elements separated by space:").split()))
# Check if the array is empty
if not array:
print("Array is empty. No elements to sort.")
return
# Calling the bubble Sort Function
sorted_array = bubbleSort(array)
# Printing the sorted array
print("Sorted Array:", sorted_array)
except ValueError as ve:
print(f"Error: {ve}")
if __name__ == "__main__":
main()
- Bubble Sort is not adaptive. Its performance remains the same regardless of the initial order of elements. It performs the same number of comparisons and swaps in every pass through the array.
Explanation:
def bubbleSort(array):
This defines a function called bubbleSort that takes a single argument, array.
for i in range(len(array)):
A for loop is used to iterate through each element in the array. The loop variable i is used to keep track of the current element being processed.
for j in range(i,len(array)-1-i):
A nested for loop is used within the bubbleSort function to compare adjacent elements in the array. The outer variable i is used to keep track of the current element being processed, and the inner variable j is used to compare adjacent elements starting from the next element after the one currently being processed. The expression len(array)-1-i is used to subtract the current index (i) from the total length of the array (len(array)).
if array[j]>array[j+1]: array[j],array[j+1]=array[j+1],array[j]
An if statement is used to compare adjacent elements in the array. If the element at index j is greater than the element at index j+1, the two elements are swapped using the tuple unpacking assignment operator =.
Example Test Cases:
- Basic Test Case:
- Input:
5 2 9 1 5 - Output:
Sorted Array: [1, 2, 5, 5, 9]
- Input:
- Empty Array Test Case:
- Input: (empty array)
- Output:
Array is empty. No elements to sort. - Explanation: The program correctly handles the case when the input array is empty.
- Already Sorted Test Case:
- Input:
1 2 3 4 5 - Output:
Sorted Array: [1, 2, 3, 4, 5]
- Input:
C++ code for Bubble Sort:
/*Copyrights to venkys.io*/
/*For more programs visit venkys.io */
/*C++ program for Bubble sort*/
//Stable: Yes
//Inplace: Yes
//Adaptive: No
//Time Complexity: Best case - O(n), Average and worst case - O(n^2)
//Space Complexity: O(1)
#include <iostream>
// Include the input/output stream header file
using namespace std;
// Namespace identifies the code is part of the standard library
void swap(int array[], int i, int j)
// Swapping function to swap two elements when compared adjacently through a temporary variable 'temp'
{
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
// Function to perform bubble sort on an array
void bubbleSort(int array[], int n)
{
// Check for null or negative array size
if (array == NULL || n <= 0)
{
cerr << "Error: Invalid array size or null pointer. Exiting.\n";
return;
}
// Outer loop: Iterate through each element in the array (except the last one)
for (int i = 0; i < n - 1; i++)
{
// Inner loop: Compare and swap adjacent elements to move the largest element to the end
for (int j = 0; j < n - i - 1; j++)
{
// Check for null pointer in array
if (array == NULL)
{
cerr << "Error: Null pointer in array. Exiting.\n";
return;
}
// Check if the current element is greater than the next element
if (array[j] > array[j + 1])
{
// Swap the current and next elements if they are in the wrong order
swap(array, j, j + 1);
}
}
}
// Display the sorted array
cout << "Sorted Array: ";
for (int k = 0; k < n; k++)
{
cout << array[k] << " "; // Print each element of the sorted array
}
cout << endl; // Move to the next line after printing the sorted array
}
int main()
{
// Prompt the user to enter the size of the array
cout << "Enter the size of the array: ";
int n; // Declare a variable 'n' to store the size of the array
// Check for invalid input (non-numeric or negative size)
if (!(cin >> n) || n <= 0)
{
cerr << "Error: Invalid input for array size. Exiting.\n";
return 1;
}
// Dynamically allocate memory for an integer array of size 'n'
int *array = new int[n];
// Prompt the user to enter the elements of the array
cout << "Enter the elements of the array: ";
// Loop to read 'n' elements and store them in the dynamically allocated array
for (int i = 0; i < n; i++)
{
// Check for invalid input (non-numeric)
if (!(cin >> array[i]))
{
cerr << "Error: Invalid input for array element. Exiting.\n";
delete[] array; // Free dynamically allocated memory before exiting
return 1;
}
}
// Calling the bubble Sort function to sort the array
bubbleSort(array, n);
delete[] array; // Freeing allocated memory
return 0;
}
Example Test Cases:
Test case 1: Normal Input Enter the size of the array: 5 Enter the elements of the array: 3 1 5 4 2
Output: Sorted Array: 1 2 3 4 5
Test case 2: Empty Array Enter the size of the array: 0
Output: Error: Invalid array size or null pointer. Exiting.
Test case 3: Non-Numeric Input for Array Size Enter the size of the array: abc
Output: Error: Invalid input for array size. Exiting.
Java code for Bubble sort:
/*Copyrights to venkys.io*/
/*For more programs visit venkys.io */
/*Java program for Bubble sort*/
//Stable: Yes
//Inplace: Yes
//Adaptive: No
//Time Complexity: Best case - O(n), Average and worst case - O(n^2)
//Space Complexity: O(1)
import java.util.InputMismatchException; // Import the InputMismatchException class for handling input errors
import java.util.Scanner; // Importing the Scanner class from java.util package for user input
public class bubbleSort{// Declaration of the bubbleSort class
public static void VSDsort(int n,int[] a)
{
// Declaration of a static method named VSDsort that takes an integer n and an integer array a as parameters
// Null check for the array
if (a == null) {
System.out.println("Error: Input array is null.");
return;
}
for(int i=0;i<n;i++) {
// Outer loop: iterating through each element of the array
for(int j=0;j<n-i-1;j++) {
// Inner loop: iterating through the unsorted part of the array
if (a[j]>a[j+1]) {
// Checking if the current element is greater than the next element
VSDswapElementsAt(a,j+1,j);} // Calling a method to swap elements if necessary
}
}
}
// Method to swap elements at two specified positions in the array
public static void VSDswapElementsAt(int[] a,int t1,int t2)
{
{
int temp = a[t1];
a[t1] = a[t2];
a[t2] = temp;
}
}
//Function to print output
public static void VSDprintOutput(int n,int a[]) {
// Null check for the array
if (a == null) {
System.out.println("Error: Input array is null.");
return;
}
System.out.println("The sorted order is:");
for(int i=0;i<n;i++) {
System.out.print(a[i]+" ");
}
}
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);// Create a Scanner object for user input
//Input the size of the array
System.out.print("Enter the size of the array: ");
int n;
try {
n= scanner.nextInt();
} catch (InputMismatchException e) {
System.out.println("Error: Please enter valid integer for array size.");
return;
}
// Edge case: Non-positive array size
if (n <= 0) {
System.out.println("Error: Array size must be a positive integer.");
return;
}
int[] a = new int[n];
//Input the elements of the array
System.out.println("Enter the elements of the array:");
for (int i = 0; i < n; i++) {
try {
a[i] = scanner.nextInt();
} catch (InputMismatchException e) {
System.out.println("Error: Please enter valid integers for array elements.");
return;
}
}
VSDsort(n,a);//Call to sort the array
VSDprintOutput(n,a);//Printing output
}
}
Test Case 1: Basic Input
Enter the size of the array: 5 Enter the elements of the array: 4 2 7 1 5 The sorted order is: 1 2 4 5 7
Test Case 2: Array with Duplicate Elements
Enter the size of the array: 6 Enter the elements of the array: 3 1 5 2 5 1 The sorted order is: 1 1 2 3 5 5
Test Case 3: Empty Array and Negative Integer Input
Enter the size of the array: 0 Error: Array size must be a positive integer.
Test Case 6: Non-Integer Array Size Input
Enter the size of the array: abc Error: Please enter a valid integer for the array size.
Test Case 4: Non-Integer Array Element Input
Enter the size of the array: 3 Enter the elements of the array: 1 xyz 3 Error: Please enter valid integers for array elements.
