Exploring sorting technique:Bucket sort

Today, we dive into the fascinating world of sorting algorithms and uncover one of their most captivating mysteries – Bucket sort. Get ready to embark on an adventure that will challenge your mind and leave you with newfound insights into the power of sorting!

Introduction to sorting technique:

Sorting is a fundamental operation in computer science that involves arranging a collection of elements in a specific order. The order can be ascending or descending based on some defined criteria, such as numerical values or lexicographical order. Efficient sorting is crucial for optimizing various algorithms and improving the performance of search and retrieval operations. There are numerous sorting techniques, each with its own set of advantages and disadvantages, allowing developers to choose the most suitable algorithm based on the characteristics of the data and the requirements of the specific application.

Sorting algorithms can be broadly categorized into comparison-based and non-comparison-based methods. Comparison-based sorting algorithms, such as QuickSort and MergeSort, rely on comparing elements to determine their order. These algorithms generally have a time complexity of O(n log n), making them efficient for large datasets. Non-comparison-based sorting algorithms, like Radix Sort and Counting Sort, exploit specific properties of the data to achieve linear time complexities under certain conditions. The choice of a sorting technique depends on factors like the size of the dataset, the distribution of data, and the desired trade-off between time and space complexities

Bucket sort:

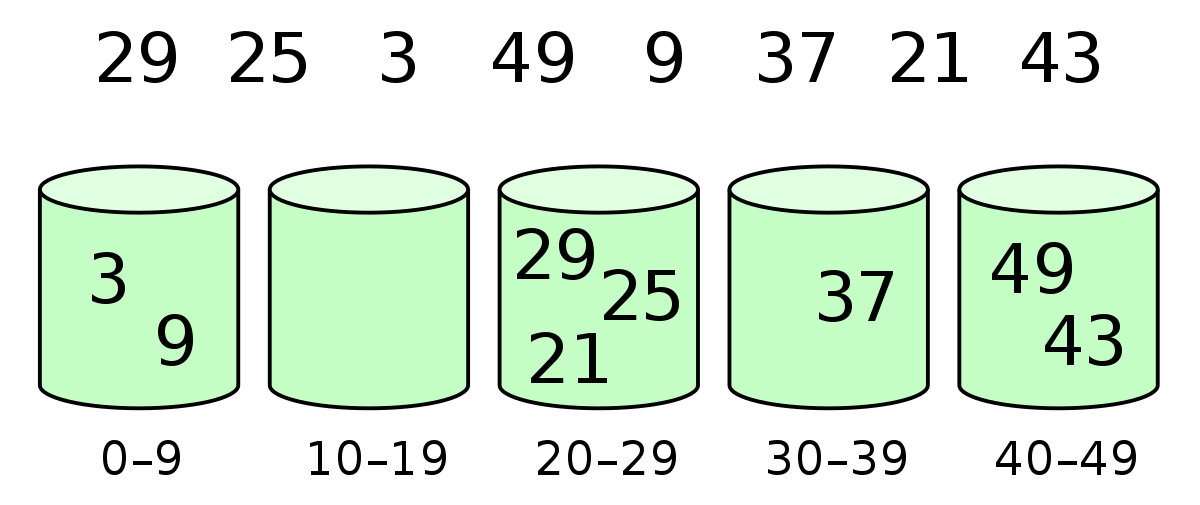
Bucket Sort is a distribution-based sorting algorithm that divides the input array into a finite number of buckets, each responsible for a specific range of values. The elements are then placed into their respective buckets based on their values. After sorting each bucket individually, the contents are concatenated to obtain the final sorted array. Bucket Sort is particularly effective when the input data is uniformly distributed across a range. By distributing elements into buckets and sorting each bucket efficiently, Bucket Sort can achieve linear time complexity in the best-case scenario. However, its performance may degrade if the input is not well-distributed or if there are too few buckets relative to the range of values.The efficiency of Bucket Sort relies on the choice of the number of buckets and the method used to sort the individual buckets. It is well-suited for scenarios where the input data is evenly spread, and the range of values is known in advance. While it may not be as versatile as some comparison-based sorting algorithms for general use cases, Bucket Sort's simplicity and linear time complexity in favorable scenarios make it a valuable tool in specific situations where its assumptions align with the characteristics of the data.

Overview of bucket sort:

Bucket Sort is a non-comparison-based sorting algorithm that operates by dividing an array into a fixed number of buckets and then sorting the elements within each bucket. The key concept is to distribute elements into these buckets based on their values, creating subsets that are individually sorted. This sorting technique is particularly effective when the input data is evenly distributed across a range. The basic premise is to minimize the effort required to sort each bucket, assuming that the data is uniformly spread.

In the first step of Bucket Sort, elements are distributed into buckets based on predefined criteria, often involving a range of values. Once the distribution is complete, each bucket is sorted individually. The sorting within the buckets can be accomplished using another sorting algorithm, such as Insertion Sort or recursively applying Bucket Sort. Finally, the sorted elements from all the buckets are concatenated to produce the final sorted array. Bucket Sort demonstrates its optimal performance when the distribution of data is even, allowing for efficient sorting within each bucket. However, its effectiveness may diminish if the input distribution is skewed or if the number of buckets is insufficient for the range of values. While Bucket Sort is not as versatile as some comparison-based sorting algorithms, its linear time complexity in favorable scenarios makes it a valuable choice for certain types of data distributions.

Code:

Python code:

# Copyrights to venkys.io for more information, visit https://venkys.io
import sys

def VSDBucketSort(arr, n):
    # Find the minimum and maximum values in the array
    mini = min(arr)
    maxi = max(arr)

    # Create 'n' buckets
    bucket = [[] for i in range(n)]

    # Distribute elements into buckets
    for i in range(n):
        # Determine the bucket index for each element based on its value
        j = n * (arr[i] - mini) // (maxi + 1 - mini)
        # Append the element to the corresponding bucket
        bucket[j].append(arr[i])

    # Sort each individual bucket
    i = 0
    for j in range(n):
        temp = bucket[j]
        temp.sort()
        # Step 5: Concatenate sorted buckets to obtain the final sorted array
        for k in range(len(temp)):
            arr[i] = temp[k]
            i += 1

    # Return the sorted array
    return arr

def main():
    try:
        # Read input values from command-line arguments
        n = int(sys.argv[1])
        arr = list(map(int, sys.argv[2:]))

        # Call the sorting function
        sorted_arr = VSDBucketSort(arr, n)

        # Print the sorted array to standard output
        print(*sorted_arr, sep=" ")

    except (ValueError, IndexError):
        print("Error: Invalid input. Please enter valid integers.")

if __name__ == "__main__":
    main()

Step-by step explanation:

Finding Min and Max: Determine the minimum (mini) and maximum (maxi) values in the input array.
Bucket Initialization: Create an array bucket containing n empty lists. These lists will serve as the buckets.
Distribution into Buckets: Iterate through the input array and distribute each element into its corresponding bucket. The formula j=n * (arr[i]-mini)//(maxi +1-mini) is used to calculate the index of the bucket for each element.
Sorting Individual Buckets: Iterate through each bucket, sort its contents, and store the sorted values back into the original buckets.
Concatenation: Concatenate the sorted buckets to obtain the final sorted array.
Print Result: Print the final sorted array.

Java code:

//Copyrights to venkys.io for more information, visit https://venkys.io
//Java program for sorting given numbers using bucket sort 
import java.util.ArrayList;

public class Main {

	static ArrayList<Integer> temp[]=new ArrayList[10];//Array of  buckets
	//Function to perform bucket sort
	public static void VSDSort(int n,int[] arr) {
		//Creating buckets to hold certain range of numbers
		for(int i=0;i<10;i++) {
			temp[i]=new ArrayList<Integer>();
		}
		//Arranging input numbers into appropriate buckets in a sorted order using insertion sort
		for(int i=0;i<arr.length;i++) {
			int t=arr[i]/10;
			int element=arr[i];
			if(temp[t].isEmpty())
				temp[t].add(element);
			else if(element>temp[t].get(temp[t].size()-1))
				temp[t].add(element);
			else if(element< temp[t].get(0)) {
				for(int j=temp[t].size()-1;j>=0;j--)
				{	if(j+1==temp[t].size())
					temp[t].add(j+1,temp[t].get(j));
					else
					temp[t].set(j+1,temp[t].get(j));
				}
				temp[t].set(0, element);
				}
			else
			{
				for(int j=0;j<temp[t].size();j++) {
					if(element>temp[t].get(j)&&element<temp[t].get(j+1)) {
						for(int k=temp[t].size()-1;k>=j;k--) 
						{	if(k+1==temp[t].size())
								temp[t].add(k+1,temp[t].get(k));
							else
							temp[t].set(k+1,temp[t].get(k));
						}
						temp[t].set(j+1, element);
						}
				}
			}
		}
	}

	//Function to print output
	public static void VSDprintOutput() {
		System.out.println("The sorted order is:");
		for(int i=0;i<temp.length;i++) {
			for(int k=0;k<temp[i].size();k++) {
				System.out.print(temp[i].get(k)+" ");
				
			}
		}
		System.out.println();
	}
	public static void main(String args[]) {
	int[] a={1, 2, 53, 12, 45, 11, 56};
	int n=a.length;
	VSDSort(n,a);
	VSDprintOutput();
	}
}

Step-by step explanation:

Bucket Initialization: Create an array of arraylist (buckets) to represent the buckets. Each bucket will store elements falling within a certain range.
Distribution into Buckets: Iterate through the input array and distribute each element into its corresponding bucket based on the scaled value.
Sorting Individual Buckets: Sort each individual bucket using a sorting method. In this case, collections.sort() is used.
Concatenation: Concatenate the sorted buckets to obtain the final sorted array.
Application of Bucket Sort: Call the bucketsort() method to sort the input array.
Print Result: Print the final sorted array.

C++ code:

// Copyrights to venkys.io for more information, visit https://venkys.io
#include<iostream>
#include<vector>
#include<bits/stdc++.h>

using namespace std;

// Function to find the minimum value in the array
int min(int arr[], int n) {
    int mini = arr[0];
    for (int i = 0; i < n; i++) {
        if (arr[i] < mini)
            mini = arr[i];
    }
    return mini;
}

// Function to find the maximum value in the array
int max(int arr[], int n) {
    int maxi = arr[0];
    for (int i = 0; i < n; i++) {
        if (arr[i] > maxi)
            maxi = arr[i];
    }
    return maxi;
}

// Bucket Sort function
void bucketSort(int arr[], int n) {
    // Step 1: Find the minimum and maximum values in the array
    int mini = min(arr, n);
    int maxi = max(arr, n);

    // Step 2: Create a vector of vectors to represent the buckets
    vector<vector<int>> bucket(n);

    // Step 3: Distribute elements into buckets
    for (int i = 0; i < n; i++) {
        int j = n * (arr[i] - mini) / (maxi + 2 - mini);
        bucket[j].push_back(arr[i]);
    }

    // Step 4: Sort each individual bucket
    int i = 0;
    for (int j = 0; j < n; j++) {
        vector<int> bj = bucket[j];
        sort(bj.begin(), bj.end());
        // Step 5: Concatenate sorted buckets to obtain the final sorted array
        for (int k = 0; k < bj.size(); k++) {
            arr[i++] = bj.at(k);
        }
    }
}

int main() {
    // Step 6: Example usage in the main function
    int arr[] = {5, 2, 9, 12, 54, 31, 65, 31, 45, 65};
    int n = sizeof(arr) / sizeof(arr[0]);

    // Step 7: Apply Bucket Sort
    bucketSort(arr, n);

    // Step 8: Print the sorted array
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;

    return 0;
}

Step-by-step explanation:

Find Min and Max: Find the minimum and maximum values in the array using the min and max functions.
Create Buckets: Create a vector of vectors (bucket) to represent the buckets.
Distribution into Buckets: Distribute elements into buckets based on their values.
Sorting Individual Buckets: Sort each individual bucket using the sort function from the header.
Concatenation: Concatenate the sorted buckets to obtain the final sorted array.
Example Usage: In the main function, an example array is sorted using the bucketsort function.
Print Result: Print the final sorted array.

Time and Space complexity analysis:

Time Complexity:
- In the average case, where the input data is uniformly distributed across the buckets, the time complexity of Bucket Sort is often considered linear, O(n + n^2/k + k), where n is the number of elements, and k is the number of buckets. The dominant term is usually the sorting of individual buckets.
- The worst-case time complexity occurs when all elements are placed in a single bucket, making the algorithm degrade to the time complexity of the sorting algorithm used for the individual buckets (typically O(n log n) for a good sorting algorithm).
Space Complexity:
- The space complexity of Bucket Sort is primarily determined by the additional space required for the buckets. In the worst case, where each element is placed in a separate bucket, the space complexity is O(n + k), where n is the number of elements, and k is the number of buckets.
- If the number of buckets is kept constant (not proportional to the input size), the space complexity is effectively O(n).

Real world applications of bucket sort:

Data Distribution Analysis:
- Bucket Sort can be employed in statistical analysis to distribute and categorize data into ranges. This is helpful in understanding the distribution of data across various intervals.
Histogram Sorting:
- In image processing and computer graphics, Bucket Sort can be used to sort pixel values into bins, facilitating the creation of histograms. Histograms are essential for various image enhancement and analysis techniques.
Radix Sort Building Block:
- Bucket Sort is often used as a building block for Radix Sort, a more complex sorting algorithm. Radix Sort is particularly efficient for sorting integers with multiple digits or keys.
Database Indexing:
- In database management systems, Bucket Sort can be applied to distribute data into buckets based on specific criteria. This can aid in creating indexes for faster data retrieval.
External Sorting:
- When dealing with large datasets that don't fit entirely into memory, Bucket Sort can be adapted for external sorting. In this context, the buckets represent chunks of data that can be sorted independently before merging the results.
Network Traffic Management:
- In networking, particularly in Quality of Service (QoS) applications, Bucket Sort can be used to categorize packets based on their priority levels, allowing for efficient traffic management.
Load Balancing:
- In distributed computing or parallel processing environments, Bucket Sort can be employed for load balancing by distributing tasks among processing units based on specific criteria.
Digital Signal Processing:
- In signal processing applications, Bucket Sort can be utilized for sorting data samples into frequency bins, aiding in the analysis and processing of signals.