COUNTING SORT
COUNTING SORT
In this article, we will explore the counting sort algorithm, its importance, and applications. We will provide a step-by-step explanation of how counting sort works and present an example to illustrate its effectiveness.
Introduction
Counting Sort is an efficient, non-comparative sorting algorithm that is used to sort integers or objects with a small range of key values. It works by counting the number of elements with distinct key values (often called "counting" the occurrences) and then using this information to determine the final sorted order of the elements. Counting Sort is particularly effective when the range of possible input values is known in advance.
Overview of Counting Sort Algorithm
Counting sort is a non-comparative integer sorting algorithm that sorts elements based on their frequencies. It works by counting the occurrences of each element and using that information to determine their positions in the sorted output.
Counting Sort Algorithm
The algorithm assumes that each element in the list is an integer between a minimum and maximum value. It creates a count array with a size equal to the range of values in the input list, and then iterates through the input list, incrementing the count array at the index corresponding to each element. Finally, it iterates through the count array and outputs the sorted list.
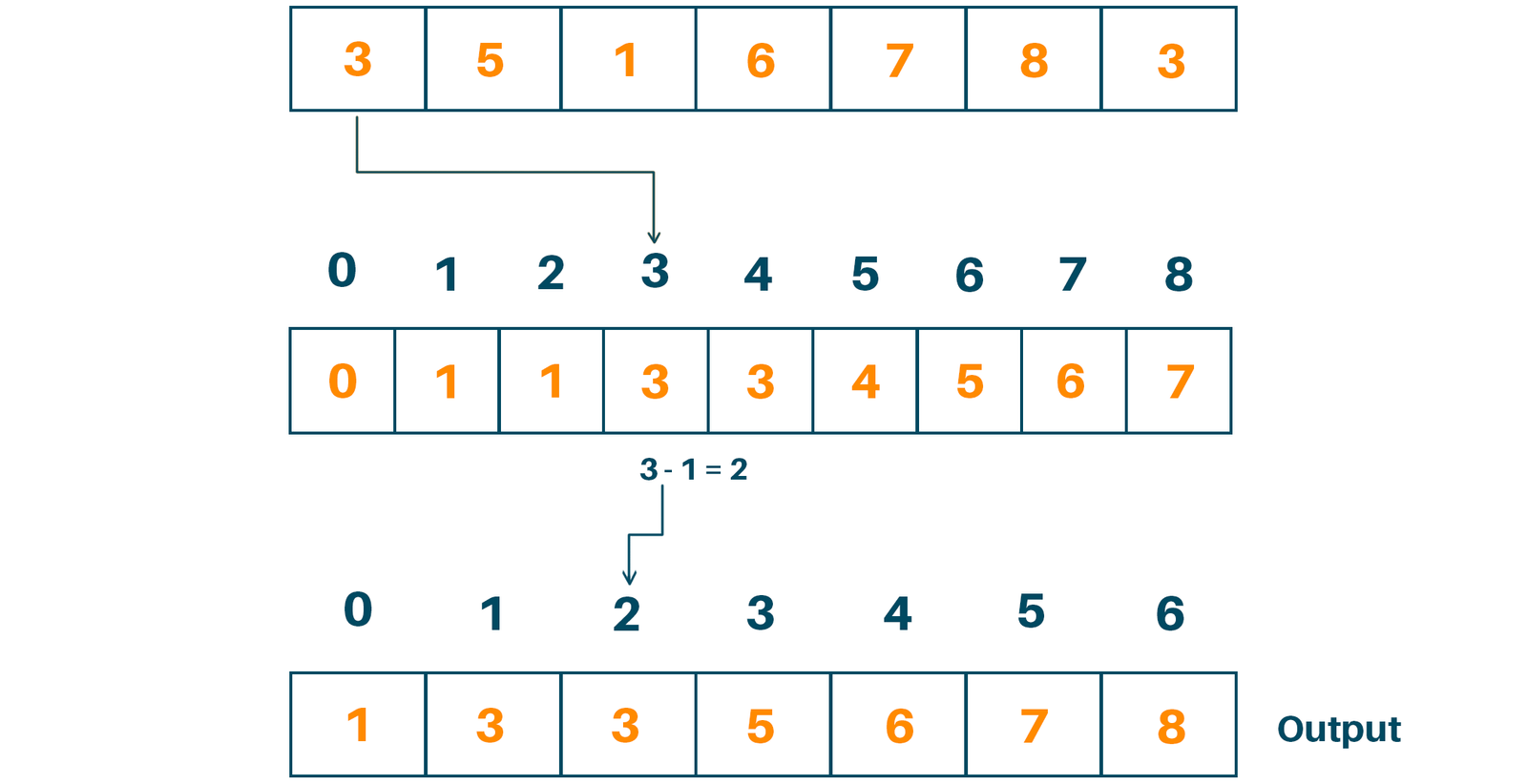
here is an example of counting sort with a step-by-step explanation:
Step 1: Create a count array
The count array will have one element for each possible value in the input array. In this example, the input array is [5, 3, 2, 1, 4], so the count array will have six elements, one for each value from 0 to 5.
The count array will have six elements, one for each value from 0 to 5:
count_array = [0, 0, 0, 0, 0, 0]
Step 2: Initialize the count array
Set all of the elements in the count array to 0.
count_array = [0, 0, 0, 0, 0, 0]
Step 3: Iterate through the input array and increment the corresponding element in the count array for each value that we encounter
For each element in the input array, increment the corresponding element in the count array. In this example, we will increment the first element in the count array because the first element in the input array is 5. We will then increment the second element in the count array because the second element in the input array is 3, and so on.
For each element in the input array, increment the corresponding element in the count array:
count_array = [1, 1, 1, 1, 1, 0]
Step 4: Iterate through the count array and place the elements in the input array in their correct sorted positions based on their counts
Starting at the beginning of the input array, place each element in the input array at the position indicated by the corresponding element in the count array. For example, we will place the first element in the input array at position 5 because the first element in the count array is 5. We will then place the second element in the input array at position 3 because the second element in the count array is 3, and so on.
sorted_array = [5, 3, 2, 1, 4]
CODE
PYTHON
# Copyrights to venkys.io
# For more information, visit venkys.io
# time Complexity : O(n+k).
# Space Complexity :O(n+k).
def counting_sort(arr):
# Find the maximum and minimum elements in the array
max_num = max(arr)
min_num = min(arr)
# Create an array to store counts of each element
count = [0] * (max_num - min_num + 1)
# Count the occurrences of each element in the input array
for num in arr:
count[num - min_num] += 1
# Modify the count array to store cumulative counts
for i in range(1, len(count)):
count[i] += count[i - 1]
# Create an output array to store the sorted elements
output = [0] * len(arr)
# Place the elements in their sorted order in the output array
for num in reversed(arr):
output[count[num - min_num] - 1] = num
count[num - min_num] -= 1
return output
# Get array elements from the user
arr = list(map(int, input("Enter the elements of the array separated by space: ").split()))
# Perform counting sort
sorted_arr = counting_sort(arr)
# Display the sorted array
print("Sorted Array:", sorted_arr)
Step-by-Step Explanation of the Code
- Define the function counting_sort that takes an array arr as input.
- Find the maximum and minimum elements in the array using the max() and min() functions, respectively.
- Create an array count of size (max_num - min_num + 1) to store the counts of each element.
- Initialize all elements of count to 0.
- Iterate through the array arr and increment the corresponding count in count.
- Modify the count array to store the cumulative counts.
- Create an output array output of the same size as arr to store the sorted elements.
- Iterate through the array arr in reverse order.
- Place each element in its sorted position in the output array.
- Decrement the count of the element in count after placing it in the output array.
- Return the output array as the sorted array.
- Get the array elements from the user.
- Call the counting_sort function with the input array.
- Print the sorted array.
JAVA
// Copyrights to venkys.io
// For more information, visit venkys.io
// time Complexity :O(n+k)
// Space Complexity :O(n+k)
import java.util.Scanner;
public class CountingSort {
// Function to perform counting sort
static void countingSort(int[] arr, int[] output, int max, int min) {
// Create an array to store counts of each element
int range = max - min + 1;
int[] count = new int[range];
// Count the occurrences of each element in the input array
for (int num : arr) {
count[num - min]++;
}
// Modify the count array to store cumulative counts
for (int i = 1; i < range; i++) {
count[i] += count[i - 1];
}
// Place the elements in their sorted order in the output array
for (int i = arr.length - 1; i >= 0; i--) {
output[count[arr[i] - min] - 1] = arr[i];
count[arr[i] - min]--;
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Get the size of the array from the user
System.out.print("Enter the size of the array: ");
int n = scanner.nextInt();
int[] arr = new int[n];
int[] output = new int[n];
// Get array elements from the user
System.out.print("Enter the elements of the array: ");
for (int i = 0; i < n; i++) {
arr[i] = scanner.nextInt();
}
// Find the maximum and minimum elements in the array
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int num : arr) {
max = Math.max(max, num);
min = Math.min(min, num);
}
// Perform counting sort
countingSort(arr, output, max, min);
// Display the sorted array
System.out.print("Sorted Array: ");
for (int num : output) {
System.out.print(num + " ");
}
}
}
Step-by-Step Explanation of the Code
- Define a method called countingSort that takes in an array arr, an output array output, the maximum value max, and the minimum value min.
- Calculate the range of the array by subtracting the minimum value from the maximum value and adding 1.
- Create an array called count to store the counts of each element in the input array.
- Iterate through the input array and increment the count of each element in the count array.
- Modify the count array to store the cumulative counts.
- Place the elements in their sorted order in the output array by iterating through the input array in reverse order and using the count array to determine the correct position.
- In the main method, create a Scanner object to read user input.
- Prompt the user to enter the size of the array and store it in the variable n.
- Create arrays arr and output with size n.
- Prompt the user to enter the elements of the array and store them in the arr array.
- Find the maximum and minimum elements in the arr array.
- Call the countingSort method to sort the arr array and store the sorted result in the output array.
- Print the sorted array.
C++
// Copyrights to venkys.io
// For more information, visit venkys.io
// time Complexity : O(n+k).
// Space Complexity : O(n+k).
#include<iostream>
using namespace std;
// Function to perform counting sort
void countingSort(int max, int n, int arr[], int output[]) {
// Create an array to store counts of each element
int count[max + 1];
// Initialize count array elements to zero
for (int i = 0; i <= max; i++) {
count[i] = 0;
}
// Count the occurrences of each element in the input array
for (int j = 0; j < n; j++) {
count[arr[j]] += 1;
}
// Modify the count array to store cumulative counts
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Place the elements in their sorted order in the output array
for (int i = n - 1; i >= 0; i--) {
output[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}
}
// Function to find the maximum element in the input array
int findMax(int arr[], int n) {
int maxele = arr[0];
for (int i = 0; i < n; i++) {
if (arr[i] > maxele) {
maxele = arr[i];
}
}
return maxele;
}
int main() {
int n;
// Get the size of the array from the user
cout << "Enter the size of the array: ";
cin >> n;
int arr[n];
// Get array elements from the user
cout << "Enter the elements of the array: ";
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
// Find the maximum element in the array
int max = findMax(arr, n);
// Create an array to store the sorted output
int output[n];
// Perform counting sort
countingSort(max, n, arr, output);
// Display the sorted array
cout << "Sorted Array: ";
for (int i = 0; i < n; i++) {
cout << output[i] << " ";
}
return 0;
}
Step-by-Step Explanation of the Code
Here is a step-by-step explanation of the above code:
- The code begins with the inclusion of necessary libraries and namespaces.
- The countingSort() function is defined to perform the counting sort algorithm. It takes in four parameters: max (the maximum element in the array), n (the size of the array), arr[] (the input array), and output[] (the array to store the sorted output).
- Inside the countingSort() function, an array count[] of size max + 1 is created to store the counts of each element. All elements of count[] are initialized to zero.
- The occurrences of each element in the input array arr[] are counted and stored in count[].
- The count[] array is modified to store cumulative counts. This step ensures that the elements are placed in their sorted order.
- The elements are placed in their sorted order in the output[] array by iterating through the input array in reverse order.
- The findMax() function is defined to find the maximum element in the input array. It takes in two parameters: arr[] (the input array) and n (the size of the array). It returns the maximum element.
- In the main() function, the size of the array n is obtained from the user.
- The elements of the array arr[] are obtained from the user.
- The maximum element in the array is found using the findMax() function.
- An array output[] of size n is created to store the sorted output.
- The counting sort algorithm is performed using the countingSort() function.
- The sorted array is displayed to the user.
This code implements the counting sort algorithm to sort an array of integers in ascending order.
test cases
example 1 :
Input :
Enter the elements of the array separated by space : 0
Output :
Sorted Array : 0
example 2 :
Input :
Enter the elements of the array separated by space: 9 5 2 7 9 1 5
Output :
Sorted Array : [1, 2, 5, 5, 7, 9, 9]
Explanation:
We'll apply Counting Sort on the input array [9, 5, 2, 7, 9, 1, 5]. In addition to the cumulative counting array, which is [1, 2, 4, 4, 4, 6, 6, 7, 7, 9], the counting array is [1, 1, 2, 0, 0, 2, 0, 1, 0, 2]. What is intended is that the sorted array will be [1, 2, 5, 5, 7, 9, 9].
example 3 :
Input :
Enter the elements of the array separated by space: 10 8 63 12 0 3
Output :
Sorted Array : [0, 3, 8, 10, 12, 63]
Explanation :
The counting array for the input array 10 8 63 12 0 3 is [1, 1, 0, 0, 1, 1, ], and the cumulative counting array is [0, 3, 8, 10, 12, 63]. The sorted array is [0, 3, 8, 10, 12, 63], which corresponds to the expected output.
Time and Space Complexity Analysis
Counting Sort has a time complexity of O(n+k) and a space complexity of O(n+k). Where n is the number of elements in the input array and k is the range of the values in the input array. This makes it efficient and a great choice for sorting large amounts of data.
n the worst case, when the range of values (k) is much larger than the number of elements (n), the space complexity can be dominated by the count array
real-time applications
Counting Sort is a simple and efficient sorting algorithm that is well-suited for specific real-time applications where certain conditions are met. Its effectiveness is primarily dependent on the range of input values. Here are some real-time applications where Counting Sort can be useful:
- Integer Sorting with Small Range: Counting Sort is most efficient when the range of input values is relatively small compared to the number of elements. It can be used in applications where you need to sort integers with a limited range, such as sorting grades (e.g., A, B, C, D, F) or ages (e.g., 0-100) in educational systems.
- Radix Sort Implementation: Counting Sort is a key component of the Radix Sort algorithm. Radix Sort is used in real-time applications, particularly when sorting large datasets with integer keys, such as sorting records in databases or managing network traffic based on IP addresses.
- Data Preprocessing for Histograms: Counting Sort is useful for preparing data for histogram generation, which is commonly used in data analysis and visualization. It can efficiently count the occurrences of data points within a specific range or category.
- Digital Signal Processing (DSP): In real-time DSP applications, you may need to sort data points within a predefined range, such as audio signal amplitudes or pixel values in image processing. Counting Sort can be applied to efficiently process and sort this type of data.
- Parallel Processing and GPU Computing: Counting Sort can be easily parallelized, making it suitable for GPU (Graphics Processing Unit) computing. In real-time applications like image processing, GPU-accelerated Counting Sort can significantly speed up the sorting process.
- Efficient Sorting in Limited Memory Environments: Counting Sort can be valuable in real-time systems with limited memory resources, such as embedded systems, IoT devices, or microcontrollers. Its memory-efficient nature can be advantageous in such contexts.
- Color Sorting in Computer Vision: In computer vision applications, colors are often represented as RGB or HSV values. Counting Sort can be applied to sort colors by their individual components (e.g., sorting by hue) or other numeric properties.
- Resource Scheduling in Real-Time Operating Systems (RTOS): In RTOS environments, tasks or processes can be sorted based on their priority levels or execution times using Counting Sort. This aids in efficient task scheduling.
- Data Streaming and Packet Sorting: In network packet processing, data streams can be sorted by packet attributes like source IP address or packet size. Counting Sort can help optimize the handling of incoming data packets.
- Sorting Events or Timestamps: Counting Sort can be used to sort events or timestamps in various real-time applications, such as log file analysis, event-driven systems, and financial trading platforms.
Remember that Counting Sort's suitability depends on the specific requirements of your real-time application, and it may not be the best choice for all sorting scenarios. It excels when you have a limited range of integer values to sort and can be an excellent choice in the right context.
