Exploring Tree Algorithms: Deleting Nodes in Binary Search Trees

Embark on a journey deeper into the fascinating realm of Binary Search Trees (BSTs) as we delve into the intricacies of deleting nodes. Join us in understanding how this essential operation maintains the structure and integrity of BSTs.

Introduction to Tree Algorithms

Tree algorithms are an essential part of data structures in computer science. As they are used to organize and manipulate hierarchical data structures, they are a crucial tool in many applications. Among these tree designs, Binary find Trees stand out due to their superior ability to find and organize data.

A left child and a right child are the maximum number of children that can exist for each node in a Binary Search Tree (BST) data structure. Nodes in the right subtree have values greater than those of the parent node, whereas nodes in the left subtree have values lower than the parent node's. This is what a BST is fundamentally like.

The Essence of Binary Search Tree Deletion

In the life cycle of a Binary Search Tree, deletion is a crucial process that requires finesse to preserve the inherent order. Deleting a node involves considerations for nodes with zero, one, or two children, and the ultimate goal is to uphold the sorted nature of the tree.

Overview of Binary Search Tree Deletion

Deleting a node in a Binary Search Tree (BST) involves:

Identify Node:
- Locate the node to delete through a search operation.
Handle Deletion:
- For nodes with no/one child, remove or bypass.
- For nodes with two children, replace with in-order successor/predecessor.
Maintain BST Properties:
- Ensure the tree remains a valid BST after deletion.
Complexity:
- Balanced trees: Efficient deletion (log N).
- Unbalanced trees: Potential for longer deletion times (up to N).
Importance of Balance:
- Balanced trees ensure quicker and reliable deletion performance.

BST deletion is a careful process balancing removal and maintaining order, with efficiency depending on tree balance.

Node Deletion Scenarios

1. Node with No Children (Leaf Node):

If a node has no children (like a leaf), just take it out of the tree.
If the node is the starting point (root) and doesn't have a parent, removing it leaves the tree empty.
If the node has a parent, disconnect it by making the parent "forget" about it.

2. Node with One Child:

If a node has only one child, smoothly skip it by connecting its parent directly to its child.
This involves adjusting the connections to keep the tree in order.

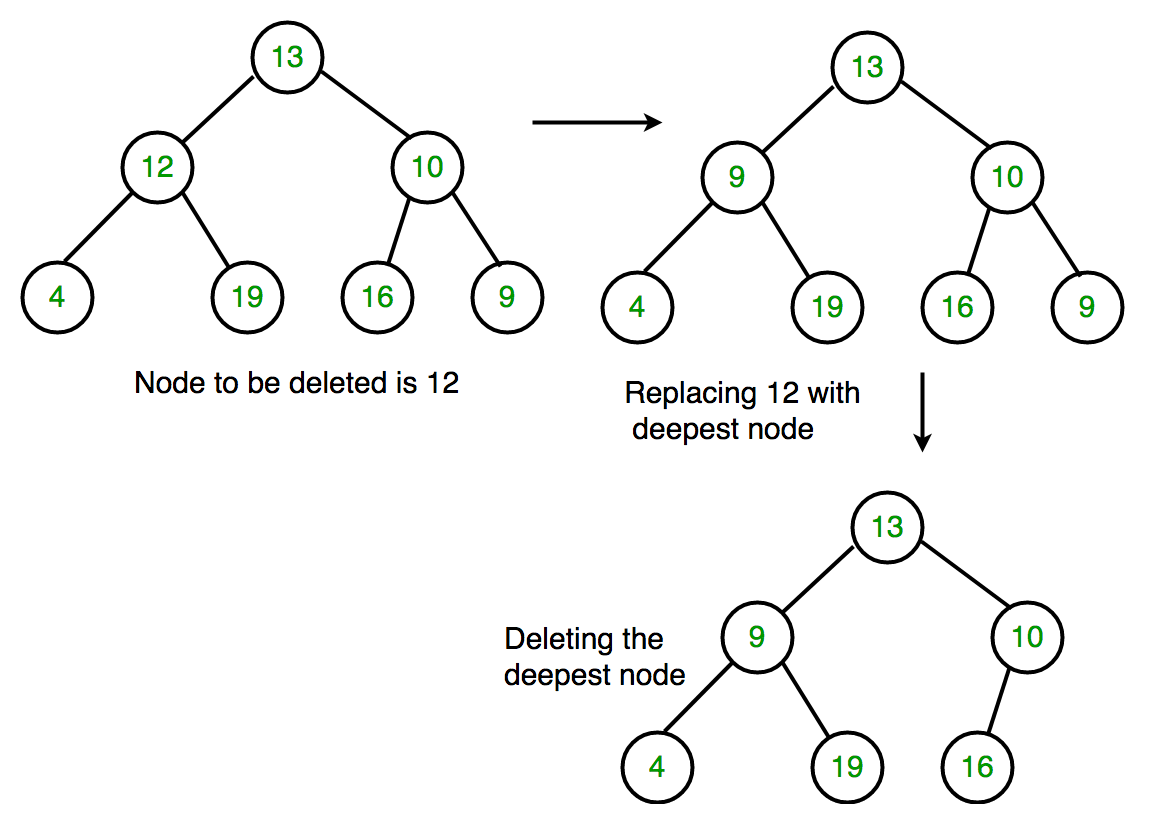
3. Deleting a Node with Two Children:

Removing a node with two children is a bit complex.
Find a good replacement node to keep the tree organized; often, choose the smallest from the right or the largest from the left.
Swap the node to be deleted with this replacement.
Now, delete the replacement, which has at most one child, following the previous rules.

Sample Test Cases


6

50 20 30 70 40 10

20


7

10 20 30 70 60 40 90

80

Python Code


# Copyrights to venkys.io

# For more information, visit https://venkys.io 



# Python Program for Binary Search Tree (BST) Deletion

# Stable: No (Deletion can change the tree structure)

# Inplace: Yes (Deletion is performed within the existing tree structure)

# Adaptive: No (Deletion complexity is not dependent on the input)



# Space complexity: O(n) (where n is the number of nodes in the tree)

# Time complexity: O(n^2)



# Node class

class Node:

    def __init__(self, data):

        

        self.data = data  # Value of the node

        self.left = self.right = None  # Pointers to the left and right child nodes





def insertBST(root, data):

    # Function to insert a new node with data into the BST



    if root is None:

        # If the tree is empty, create a new node with the given data

        return Node(data)

    if root.data == data:

        # If the data is already present in the tree, return the current root

        return root

    elif data < root.data:

        # If the data is less than the root's data, recursively insert into the left subtree

        root.left = insertBST(root.left, data)

    else:

        # If the data is greater than the root's data, recursively insert into the right subtree

        root.right = insertBST(root.right, data)

    return root





def minValue(root):

    # Function to find the node with the minimum value in a BST

    temp = root

    while temp.left:

        temp = temp.left # Traverse the left subtree until the leftmost node is reached

    return temp



# Function to delete a node with the given data from the Binary Search Tree

def deleteBST(root, data):

    if not root:

        # If the tree is empty or the node is not found, return the current root

        return root

    if data < root.data:

        # If the data is less than the root's data, recursively delete from the left subtree

        root.left = deleteBST(root.left, data)

    elif data > root.data:

        # If the data is greater than the root's data, recursively delete from the right subtree

        root.right = deleteBST(root.right, data)

    else:

        # If the node with the data is found

        if not root.left:

            # If the node has no left child, replace it with its right child

            return root.right

        elif not root.right:

            # If the node has no right child, replace it with its left child

            return root.left

        temp = minValue(root.right)

        # If the node has both left and right children, replace it with the minimum value node from the right subtree

        root.data = temp.data

        root.right = deleteBST(root.right, temp.data)

    return root



# Function to perform in-order traversal of the Binary Search Tree and print the values

def inorder(root):

    if root:

        inorder(root.left)

        print(root.data, end=" ")  # Print the value of the current node

        inorder(root.right)



# Main section

if __name__ == "__main__":

    root = None  # Initialize an empty BST



    # Taking input

    n=int(input())

    arr=[int(x) for x in input().split()][:n]

    key=int(input())



    for i in arr:

        root = insertBST(root, i)  # Insert elements into the BST



    # print("In-order traversal of the BST:")

    inorder(root)  # Print the in-order traversal of the BST

    print()



    root = deleteBST(root, key)  # Delete node with value 

    # print("In-order traversal after deleting node:")

    inorder(root)  # Print the in-order traversal after deletion

Step-by-Step Explanation of Python Code

Node class

The Node class defines a node in a Binary Search Tree (BST). Each node contains a data value and pointers to its left and right child nodes, initially set to None.
insertBST Function

The insertBST function adds a new element to the BST. If the tree is empty (no root), it makes a new node with the provided data. If the data is already in the current node, it keeps the tree unchanged. Otherwise, it recursively puts the data in the left or right subtree, depending on the comparison with the current node.
minValue Function

The minValue function finds the node with the minimum value in a BST. It traverses the left subtree until the leftmost node is reached.
deleteBST Function Overview

Deletes a node with the given data from the BST.If the tree is empty or the node is not found, it returns the current root.If the data is less than the root's data, it recursively deletes from the left subtree.If the data is greater, it deletes from the right subtree.
- Node replacement conditions if the node is found:
  - If it has no left child, replace it with its right child.
  - If it has no right child, replace it with its left child.
  - If it has both left and right children, replace it with the minimum value node from the right subtree.
inorder Function

The inorder function performs an in-order traversal of the BST, printing the values of each node in ascending order. It recursively explores the left subtree, prints the current node's data, and then recursively traverses the right subtree.
Main Section:
- Insert elements from array arr into a Binary Search Tree (BST) using insertBST.
- Print the BST values in ascending order through in-order traversal.
- Delete the node with the value from the BST using deleteBST.
- Print the in-order traversal again, showing the modified BST after deletion.

Java Code


/*Copyrights to venkys.io

For more information, visit https://venkys.io */



// Java Program for Binary Search Tree (BST) Deletion

// Stable: No (Deletion can change the tree structure)

// Inplace: Yes (Deletion is performed within the existing tree structure)

// Adaptive: No (Deletion complexity is not dependent on the input)



// Space complexity: O(n) (where n is the number of nodes in the tree)

// Time complexity: O(n^2)



import java.util.Scanner;



//Node Class

class Node {

    int data;

    Node left, right; 



    Node(int data) {

        this.data = data; // Initialize the data of the node

    }

}



public class Main {

    // Function to insert an element into a BST

    static Node insertBST(Node root, int data) {

        if (root == null)

            // Create a new node if the tree is empty

            return new Node(data); 

        if (root.data == data)

            // Return the current root if data matches

            return root; 

        else if (data < root.data)

            // Recursively insert into the left subtree

            root.left = insertBST(root.left, data); 

        else

            // Recursively insert into the right subtree

            root.right = insertBST(root.right, data);

        // Return the updated root of the tree 

        return root; 

    }



    // Function to find the minimum node in a BST

    static Node minValue(Node root) {

        Node temp = root;

        while (temp.left != null)

            temp = temp.left; // Traverse the left subtree until the leftmost node is reached

        return temp; // Return the minimum node

    }



    // Function to delete a node with the given data from a BST

    static Node deleteBST(Node root, int data) {

        if (root == null)

            // If the tree is empty or the node is not found, return the current root

            return root; 

        if (data < root.data)

            // Recursively delete from the left subtree

            root.left = deleteBST(root.left, data); 

        else if (data > root.data)

            // Recursively delete from the right subtree

            root.right = deleteBST(root.right, data); 

        else {

            if (root.left == null)

                // If the node has no left child, replace it with its right child

                return root.right; 

            else if (root.right == null)

                // If the node has no right child, replace it with its left child

                return root.left; 

            Node temp = minValue(root.right);

            // Replace the node to be deleted with the minimum value node from the right subtree

            root.data = temp.data; 

            // Recursively delete the minimum value node

            root.right = deleteBST(root.right, temp.data); 

        }

        // Return the updated root of the tree

        return root; 

    }



    // Function to perform an in-order traversal of a BST

    static void inorder(Node root) {

        if (root != null) {

            inorder(root.left);  // Recursively traverse the left subtree

            System.out.print(root.data + " ");  // Print the data in the current node

            inorder(root.right);  // Recursively traverse the right subtree

        }

    }



    public static void main(String[] args) {

        // Scanner class is used for taking input

        Scanner sc = new Scanner(System.in);



        // System.out.print("Enter the number of elements: ");

        int n = sc.nextInt();



        //Array to store n elements

        int[] arr = new int[n];

        // System.out.println("Enter the elements:");

        for (int i = 0; i < n; i++) {

            arr[i] = sc.nextInt(); // Insert elements into array

        }



        Node root = null; // Initialize an empty root for the BST



        // Insert each element from the array into the BST

        for (int i : arr) {

            root = insertBST(root, i);

        }



        // Print the in-order traversal of the BST

        // System.out.println("In-order traversal of the BST:");

        inorder(root); 

        System.out.println();



        // Delete an element in the BST

        // System.out.print("Enter the key to delete: ");

        int key = sc.nextInt();

        root = deleteBST(root, key); // Delete the node with value

        

        // Print the in-order traversal after deletion

        // System.out.println("In-order traversal after deleting node:");

        inorder(root); 

    }

}

Step-by-Step Explanation of Java Code

Node Class

This class defines a Node for a binary tree. Each node has an integer data value, a reference to the left child (left), and a reference to the right child (right).
Main Class

This is the main class that contains the main method and functions to manipulate the Binary Search Tree (BST).
insertBST Method

This function inserts a new element into the Binary Search Tree (BST). It recursively compares the data with the current node and inserts it into the left subtree if the data is less or the right subtree if the data is greater.
minValue Method

This function finds and returns the minimum value node in a BST by traversing the left subtree until the leftmost node is reached.
deleteBST Method

This function deletes a node with the given data from a BST. It handles three cases: a node with no children, a node with one child, and a node with two children.
inorder Method

This function performs an in-order traversal of the BST, printing the values in ascending order.
Main Method

In the main method, an array of integers is inserted into the BST using the insertBST function. It then prints the in-order traversal of the original BST, deletes a node with value using the deleteBST function, and prints the in-order traversal again after the deletion.

CPP Code


// Copyrights to venkys.io

// For more information, visit https://venkys.io 



// CPP Program for Binary Search Tree (BST) Deletion

// Stable: No (Deletion can change the tree structure)

// Inplace: Yes (Deletion is performed within the existing tree structure)

// Adaptive: No (Deletion complexity is not dependent on the input)



// Space complexity: O(n) (where n is the number of nodes in the tree)

// Time complexity: O(n^2) 



#include<iostream>



// Node class 

class Node {

public:

    int data;           // Data of the node

    Node *left = NULL;  // Pointer to the left child

    Node *right = NULL; // Pointer to the right child



    // Constructor to initialize a node

    Node(int val) {

        data = val;

    }

};



// Function to insert a node with given data into a BST

Node* insertBST(Node* root, int data) {

    // If the tree is empty, create a new node with the given data

    if (root == NULL)

        return new Node(data);

    // If the data matches the current node's data, return the root

    if (root->data == data)

        return root;

    // If the data is less than the current node's data, insert into the left subtree

    else if (data < root->data)

        root->left = insertBST(root->left, data);

    // If the data is greater, insert into the right subtree

    else

        root->right = insertBST(root->right, data);

    // Return the updated root of the tree

    return root;

}



// Function to find the node with the minimum value in a BST

Node* minValue(Node* root) {

    Node* temp = root;

    while (temp->left)

        temp = temp->left; // Traverse the left subtree until the leftmost node is reached

    return temp;          // Return the minimum value node

}



// Function to delete a node with the given data from a BST

Node* deleteBST(Node* root, int data) {

    // If the tree is empty or the node is not found, return the current root

    if (!root)

        return root; 

    if (data < root->data)

        root->left = deleteBST(root->left, data); // Recursively delete from the left subtree

    else if (data > root->data)

        root->right = deleteBST(root->right, data); // Recursively delete from the right subtree

    else {

        // If the node has no left child, replace it with its right child

        if (!root->left)

            return root->right;

        // If the node has no right child, replace it with its left child 

        else if (!root->right)

            return root->left; 

        Node* temp = minValue(root->right);

        // Replace the node to be deleted with the minimum value node from the right subtree

        root->data = temp->data; 

        root->right = deleteBST(root->right, temp->data); // Recursively delete the minimum value node

    }

    // Return the updated root of the tree

    return root;

}



// In-order traversal of a BST 

void inorder(Node* root) {

    if (root != NULL) {

        inorder(root->left);        // Recursively traverse the left subtree

        std::cout << root->data << " "; // Print the data in the current node

        inorder(root->right);       // Recursively traverse the right subtree

    }

}



// Main function

int main() {

    int n;

    // std::cout << "Enter the number of elements: ";

    std::cin >> n;



    int arr[n]; //Array to store n elements

    // std::cout << "Enter the elements: ";

    for (int i = 0; i < n; i++) {

        std::cin >> arr[i]; // Insert elements into array

    }



    Node* root = NULL;  // Initialize an empty root for the BST



    // Insert each element from the array into the BST

    for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {

        root = insertBST(root, arr[i]);

    }



    // Print the in-order traversal

    // std::cout << "In-order traversal of the BST: ";

    inorder(root);

    std::cout << std::endl;



    // Taking input to delete for an element in the BST

    int key;

    // std::cout << "Enter the key to delete: ";

    std::cin >> key;



    // Delete the node with value 

    root = deleteBST(root, key);



    // Print the in-order traversal after deletion

    // std::cout << "In-order traversal after deleting node:" << std::endl;

    inorder(root);



    return 0; 

}

Step-by-Step Explanation of CPP Code

<bits/stdc++.h> includes most standard C++ libraries, and is specifically for input and output operations.
Node Class

The Node class defines a node in a Binary Search Tree (BST). Each node has a data field, and pointers to its left and right child nodes, initially set to NULL.
insertBST Function
- The insertBST function inserts a new node with the given data into the BST.
- If the tree is empty (root is NULL), it creates a new node.
- If the data matches the current node, it returns the current root to avoid duplicates.
- If the data is less than the current node's data, it recursively inserts into the left subtree.
- If the data is greater, it recursively inserts into the right subtree.
minValue Function

The minValue function finds the node with the minimum value in a BST. It traverses the left subtree until the leftmost node is reached and returns that node.
deleteBST Function
- The deleteBST function deletes a node with the given data from the BST.
- If the tree is empty or the node is not found, it returns the current root.
- If the data is less than the root's data, it recursively deletes from the left subtree.
- If the data is greater, it deletes from the right subtree.
- If the node is found, it handles three cases:
  - If it has no left child, it replaces it with its right child.
  - If it has no right child, it replaces it with its left child.
  - If it has both left and right children, it replaces it with the minimum value node from the right subtree.
inorder Function
- The inorder function performs an in-order traversal of the BST.
- It recursively traverses the left subtree, prints the data in the current node, and then recursively traverses the right subtree.
Main Section
- Initializes an empty root for the BST.
- Inserts each element from the array into the BST using insertBST.
- Prints the in-order traversal of the BST.
- Deletes the node with the value from the BST using deleteBST.
- Prints the in-order traversal again, showing the modified BST after deletion.

Time and Space Complexity

Time Complexity:

Insertion (per element):
- Average Case: O(log N) - balanced tree
- Worst Case: O(N) - unbalanced tree
Deletion (per element):
- Average Case: O(log N) - balanced tree
- Worst Case: O(N) - unbalanced tree
In-order Traversal (entire tree):
- O(N) - visiting each node once

Space Complexity:

Insertion and Deletion (per element):
- Average Case: O(log N) - balanced tree
- Worst Case: O(N) - unbalanced tree
In-order Traversal (entire tree):
- O(N) - space required for the recursive call stack

Real-World Applications of Binary Search Tree Deletion

Database Management Systems: Deleting records from a database.
File System Maintenance: Removing files or directories from a file system.
Contact and Customer Management Systems: Removing contacts or customers from a management system.
Network Routing Tables: Removing entries from routing tables in networking devices.
Dynamic Memory Management in Programming: Deallocating memory in dynamic data structures.

Test Cases:

Input:

Number of elements in the array (n):

For example, 7

Array elements:

For example, 50 30 70 20 40 60 80

Key to delete from the BST:

For example, 30

Output:

In-order traversal of the BST after insertion.

In-order traversal of the BST after deletion of the specified key.

Explanation:

Input Interpretation:
- The number of elements in the array n is specified as 7.
- The array elements are 50 30 70 20 40 60 80.
- The key to delete from the BST is specified as 30.
Insertion into BST:
- The array elements are inserted into the BST using the insertBST function.
- After insertion, the BST structure might look like:
  
  50
  
  / \
30 70

/ \ / \

20 40 60 80

In-order Traversal after Insertion:

- The inorder function is called to perform an in-order traversal of the BST.

- The in-order traversal prints the nodes in non-decreasing order: 20 30 40 50 60 70 80.



Deletion of the Key:

- The deleteBST function is called to delete the node with the key 30 from the BST.

- After deletion, the BST structure might look like:

  

  50

 /  \

40 70

/ / \

20 60 80

  In-order Traversal after Deletion:

  - The inorder function is called again to perform an in-order traversal of the updated BST.

  - The in-order traversal prints the nodes in non-decreasing order after deletion: 20 40 50 60 70 80.

Conclusion

Binary search tree deletion is a crucial data structure operation, providing solutions in various applications. Proficiency in efficiently removing nodes from a BST is essential for maintaining order and optimizing processes. Whether in databases, file systems, contact management, network routing, or dynamic memory allocation in programming, the principles of BST deletion are indispensable. Just like BST searching, mastering deletion is key to creating responsive and organized software systems.