Exploring Tree Algorithms: Searching in Binary Search Trees
Exploring Tree Algorithms: Searching in Binary Search Trees
Here, we explore the intriguing world of Binary Search Trees (BSTs) and its search operations. Welcome to the world of tree algorithms. Come along on this adventure as we explore the nuances of BSTs and how they may be used to solve a range of issues.
Introduction to Tree Algorithms
A key component of data structures in computer science are tree algorithms. They are an essential tool in many applications since they are used to arrange and work with hierarchical data structures. Binary Search Trees are particularly notable among these tree designs because of how well they search and sort data.
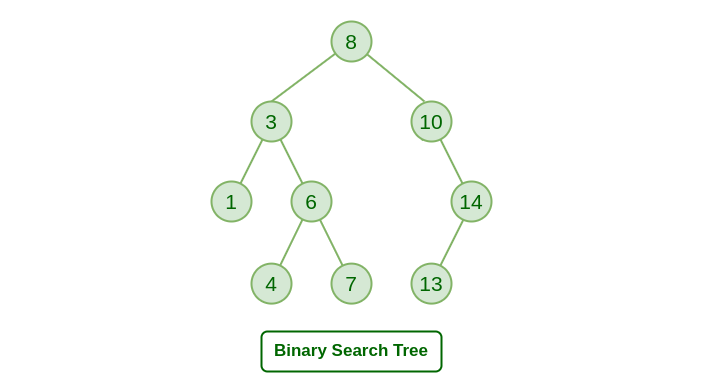
Each node in a Binary Search Tree (BST) data structure has a maximum of two children: a left child and a right child. The values of nodes in the left subtree are less than the parent node's value, while the values of nodes in the right subtree are greater than the parent node. This is the fundamental characteristic of a BST.
Binary Search Trees (BSTs)
Binary Search Trees (BSTs) are really useful for quickly finding, adding, and removing items. They're like a special kind of tree where each "branch" has only two "twigs" – one for items smaller than the currencd Codet one, and one for items larger. This makes searching for stuff super fast.
There are two types of these trees: balanced and unbalanced. Balanced ones stay organized no matter what, making them good for handling lots of items without slowing down. Unbalanced ones can get messy, especially if you add things in a specific order, and they can become slow if you're not careful.
Overview of Binary Search Tree Searching
Searching in a Binary Search Tree (BST) is like finding something in a well-organized list. We start at the top, compare what we're looking for, and decide whether to go left or right. This process repeats until we find the item or realize it's not there.
There are two ways to search: one is more like following branches until we find the thing (recursive), and the other is like moving through the list with a loop (iterative).
If the list is neat and tidy (balanced), searching is quick, usually log N time. If it's messy (unbalanced), it can take longer, up to N time in the worst case. That's why people like using BSTs for searching when things are well-organized.
Sample Test Cases
6
50 20 30 70 40 10
70
7
10 20 30 70 60 40 90
80
5
3 4 6 8 9
6
Python Code
# Copyrights to venkys.io
# For more information, visit https://venkys.io
# Python Program for Binary Search Tree (BST) Searching
# Stable: Yes (Search does not modify the tree structure)
# Inplace: No (No changes made directly to the input tree)
# Adaptive: No (Search complexity is not dependent on the input)
# Time complexity: O(log N) for average case (balanced tree), O(N) for worst case (unbalanced tree)
# Space complexity: O(log N) for average case, O(N) for worst case
# Define a class to represent a node in a binary tree
class Node:
def __init__(self, data):
self.data = data # Data stored in the node
self.left = self.right = None # Left and right child nodes
# Function to insert an element into a Binary Search Tree (BST)
def insertBST(root, data):
if root is None:
return Node(data) # Create a new node with the given data if the root is None
if root.data == data:
return root # If data matches the current node, return the root
elif data < root.data:
root.left = insertBST(root.left, data) # Insert data into the left subtree
else:
root.right = insertBST(root.right, data) # Insert data into the right subtree
return root # Return the updated root
# Function to search for a specific element in a BST
def searchBST(root, data):
if not root:
return -1 # If the root is None or the data is not found, return -1
if root.data == data:
return root # If data matches the current node, return the node
elif data < root.data:
return searchBST(root.left, data) # Search in the left subtree
elif data > root.data:
return searchBST(root.right, data) # Search in the right subtree
# Function to perform an in-order traversal of a BST
def inorder(root):
if root:
inorder(root.left) # Traverse the left subtree
print(root.data, end=" ") # Print the data in the current node
inorder(root.right) # Traverse the right subtree
# Main section
if __name__ == "__main__":
root = None # Initialize an empty root for the BST
# Taking input
n=int(input())
arr=[int(x) for x in input().split()][:n]
key=int(input())
# Insert elements into the BST
for i in arr:
root = insertBST(root, i)
# inorder(root)
# Search for an element in the BST
result = searchBST(root, key)
if result != -1:
print("Found")
else:
print("Not Found")
Step-by-Step Explanation of Python Code
-
Node Class
The
Nodeclass defines a node in a Binary Search Tree (BST). Each node has a data value and references to its left and right child nodes, initially set to None. -
insertBST Function
The
insertBSTfunction inserts a new element into the BST. If the tree is empty (root is None), it creates a new node with the given data. If the data matches the current node, it returns the root. Otherwise, it recursively inserts the data into the left or right subtree based on the comparison with the current node. -
searchBST Function
The
searchBSTfunction searches for a specific element in the BST. If the tree is empty (not root), it returns -1. If the data matches the current node, it returns the node. Otherwise, it recursively searches in the left or right subtree based on the comparison with the current node. -
inorder Function
The
inorderfunction prints the data of each node in a Binary Search Tree (BST) in ascending order through an in-order traversal. It recursively explores the left subtree, prints the current node's data, and then recursively traverses the right subtree. -
Main Section
In the main section, elements from the array
arrare inserted into a Binary Search Tree (BST) using theinsertBSTfunction. ThesearchBSTfunction is then employed to look for the element in the BST, and it prints "Found" if the element is present, otherwise "Not Found". Uncommenting theinorderfunction would print the BST elements in ascending order.
Java Code
/* Copyrights to venkys.io
For more information, visit https://venkys.io */
// Java Program for Binary Search Tree (BST) Searching
// Stable: Yes (Search does not modify the tree structure)
// Inplace: No (No changes made directly to the input tree)
// Adaptive: No (Search complexity is not dependent on the input)
// Space complexity: O(V) (where V is the number of nodes in the tree)
// Time complexity: O(V+E) (where E is the number of edges in the tree)
import java.util.Scanner;
// Define a class to represent a node in a binary tree
class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
}
}
public class Main {
// Function to insert an element into a Binary Search Tree (BST)
static Node insertBST(Node root, int data) {
// If the root is null, create a new node with the given data
if (root == null)
return new Node(data);
// If the data matches the data in the current node, return the root
if (root.data == data)
return root;
// If the data is less than the data in the current node, insert into the left subtree
else if (data < root.data)
root.left = insertBST(root.left, data);
// If the data is greater, insert into the right subtree
else
root.right = insertBST(root.right, data);
// Return the updated root of the tree
return root;
}
// Function to perform an in-order traversal of a BST
static void inorder(Node root) {
if (root != null) {
inorder(root.left); // Traverse the left subtree
System.out.print(root.data + " "); // Print the data in the current node
inorder(root.right); // Traverse the right subtree
}
}
// Function to search for a specific element in a BST
static Node searchBST(Node root, int data) {
if (root == null)
return null; // If the root is null, or the data is not found, return null
if (root.data == data)
return root; // If data matches the current node, return the node
else if (data < root.data)
return searchBST(root.left, data); // Search in the left subtree
else
return searchBST(root.right, data); // Search in the right subtree
}
public static void main(String[] args) {
// Scanner class is used for taking input
Scanner sc = new Scanner(System.in);
// System.out.print("Enter the number of elements: ");
int n = sc.nextInt();
//Array to store n elements
int[] arr = new int[n];
// System.out.println("Enter the elements:");
// Insert elements into array
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
Node root = null; // Initialize an empty root for the BST
// Insert each element from the array into the BST
for (int i : arr) {
root = insertBST(root, i);
}
// Search for an element in the BST
// System.out.print("Enter the key to search: ");
int key = sc.nextInt();
if(searchBST(root, key)!=null) System.out.println("Found");
else System.out.println("Not Found");
}
}
Step-by-Step Explanation of Java Code
-
Node Class
The
Nodeclass represents a node in a Binary Search Tree (BST). Each node has an integer data value and references to its left and right child nodes, initially set to null. -
insertBST Method
The
insertBSTmethod inserts a new element into the BST. If the tree is empty (root is null), it creates a new node with the given data. If the data matches the current node, it returns the root. Otherwise, it recursively inserts the data into the left or right subtree based on the comparison with the current node. -
inorder Method
The
inordermethod performs an in-order traversal of a BST, printing the data of each node in ascending order. It recursively traverses the left subtree, prints the current node's data, and then recursively traverses the right subtree. -
searchBST Method
The
searchBSTmethod searches for a specific element in a BST. If the tree is empty (root is null) or the data is not found, it returns null. If the data matches the current node, it returns the node. Otherwise, it recursively searches in the left or right subtree based on the comparison with the current node. -
Main Method
In the main section, an array
arris used to insert elements into the BST using theinsertBSTmethod. ThesearchBSTmethod is then used to search for the element in the BST. If found, it prints "Found"; otherwise, it prints "Not Found".
CPP Code
/* Copyrights to venkys.io
For more information, visit https://venkys.io */
// C++ Program for Binary Search Tree (BST) Searching
// Stable: Yes (Search does not modify the tree structure)
// Inplace: No (No changes made directly to the input tree)
// Adaptive: No (Search complexity is not dependent on the input)
// Space complexity: O(n)
// Time complexity: O(n)
#include<iostream>
// Define a class to represent a node in a binary tree
class Node {
public:
int data;
Node* left = NULL;
Node* right = NULL;
Node(int val) {
data = val;
}
};
// Function to insert an element into a Binary Search Tree (BST)
Node* insertBST(Node* root, int data) {
if (root == NULL)
return new Node(data); // Create a new node with the given data if the root is NULL
if (root->data == data)
return root; // If data matches the data in the current node, return the root
else if (data < root->data)
root->left = insertBST(root->left, data); // Insert data into the left subtree
else
root->right = insertBST(root->right, data); // Insert data into the right subtree
return root; // Return the updated root of the tree
}
// Function to search for a specific element in a BST
Node* searchBST(Node* root, int data) {
if (!root)
return NULL; // If the root is NULL, or the data is not found, return NULL
if (root->data == data)
return root; // If data matches the current node, return the node
else if (data < root->data)
return searchBST(root->left, data); // Search in the left subtree
else
return searchBST(root->right, data); // Search in the right subtree
}
// Function to perform an in-order traversal of a BST
void inorder(Node* root) {
if (root != NULL) {
inorder(root->left); // Traverse the left subtree
std::cout << root->data << " "; // Print the data in the current node
inorder(root->right); // Traverse the right subtree
}
}
int main() {
int n;
// std::cout << "Enter the number of elements: ";
std::cin >> n;
int arr[n]; //Array to store n elements
// std::cout << "Enter the elements: ";
for (int i = 0; i < n; i++) {
std::cin >> arr[i]; // Insert elements into array
}
Node* root = NULL; // Initialize an empty root for the BST
// Insert each element from the array into the BST
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {
root = insertBST(root, arr[i]);
}
// Taking input to search for an element in the BST
int key;
// std::cout << "Enter the key to search: ";
std::cin >> key;
// Search for an element in the BST
if(searchBST(root,key)!=NULL) std::cout<<"Found";
else std::cout<<"Not Found";
return 0;
}
Step-by-Step Explanation of CPP Code
-
Node Class
The
Nodeclass defines a node in a Binary Search Tree (BST). Each node has an integer data value and references to its left and right child nodes, initially set to NULL. -
insertBST Function
The
insertBSTfunction inserts a new element into the BST. If the tree is empty (root is NULL), it creates a new node with the given data. If the data matches the current node, it returns the root. Otherwise, it recursively inserts the data into the left or right subtree based on the comparison with the current node. -
searchBST Function
The
searchBSTfunction searches for a specific element in a BST. If the tree is empty (root is NULL) or the data is not found, it returns NULL. If the data matches the current node, it returns the node. Otherwise, it recursively searches in the left or right subtree based on the comparison with the current node. -
inorder Function
The
inorderfunction performs an in-order traversal of a BST, printing the data of each node in ascending order. It recursively traverses the left subtree, prints the current node's data, and then recursively traverses the right subtree. -
Main Function
In the main section, an array
arris used to insert elements into the BST using theinsertBSTfunction. ThesearchBSTfunction is then used to search for the element in the BST. If found, it prints "Found"; otherwise, it prints "Not Found."
Time and Space Complexity
Time Complexity: O(N) in the worst case (unbalanced tree); O(log N) on average (balanced tree).
Space Complexity: O(N) in the worst case (unbalanced tree); O(log N) on average (balanced tree).
Real-World Applications of Binary Search Tree Searching
Searching in Binary Search Trees (BSTs) is a fundamental operation with a wide range of real-world applications. Here are some practical scenarios where BST searching is valuable:
-
Databases: Many database systems use BSTs to index and search data efficiently. This allows for fast retrieval of records based on a specific key or field.
-
File Systems: File systems often employ BST-like structures to organize and search for files and directories. This hierarchical organization aids in quick file retrieval.
-
Auto-Complete and Search Engines: Auto-complete suggestions and search engines use variations of BSTs to offer quick and relevant search results to users.
-
Dictionary and Spell Checkers: Dictionaries and spell checkers can use BSTs to store and search for words efficiently, making them useful in word processing software.
-
Contact Management: Contact management applications use BSTs for organizing and searching contacts by name, phone number, or other attributes.
-
Library Catalogues: Library catalogues, whether physical or digital, can benefit from BSTs to help users locate books or resources based on various criteria.
-
Online Marketplaces: E-commerce platforms use BSTs to allow users to search for products using filters like price range, category, or brand.
-
Computer Networking: Routers and networking devices use tree-like structures, including BSTs, for routing and data lookup to determine the most efficient path for data packets.
Test Cases
-
Input: Number of elements in the array (n): For example, 6 Array elements: For example, 50 20 30 70 40 10
Key to search in the BST: For example, 40
Output: If the key is found in the BST, output: "Found" If the key is not found in the BST, output: "Not Found"
Explanation: Input Interpretation:
- The number of elements in the array n is specified as 6.
- The array elements are 50 20 30 70 40 10.
- The key to search in the BST is specified as 40.
Insertion into BST:
-
The array elements are inserted into the BST using the insertBST function.
-
After insertion, the BST structure might look like:
50 /
20 70 / \
10 30 40
Searching for the Key:
- The searchBST function is used to search for the key 40 in the BST.
- Since 40 is present in the BST, the function returns "Found".
- The output is "Found".
Final Output: The final output is "Found", indicating that the key 40 is present in the BST.
-
Input: Number of elements in the array (n): For example, 5
Array elements: For example, 30 20 40 10 50
Key to search in the BST: For example, 35
Output: If the key is found in the BST, output: "Found" If the key is not found in the BST, output: "Not Found"
Explanation:
Input Interpretation:
- The number of elements in the array n is specified as 5.
- The array elements are 30 20 40 10 50.
- The key to search in the BST is specified as 35.
Insertion into BST:
-
The array elements are inserted into the BST using the insertBST function.
-
After insertion, the BST structure might look like:
30 /
20 40 / \
10 - 50Searching for the Key:
- The searchBST function is used to search for the key 35 in the BST.
- Since 35 is not present in the BST, the function returns "Not Found".
- The output is "Not Found".
Final Output: The final output is "Not Found", indicating that the key 35 is not present in the BST.
Conclusion
Binary search trees are strong data structures with many applications that provide effective search functions. One of the most important computer science skills is knowing how to search in a BST, which may be used to solve a wide range of real-world issues. The concepts of Binary Search Tree Searching are useful tools to have in your toolbox whether you deal with databases, compilers, or any other software system that requires searching.
