FLATTEN BINARY TREE
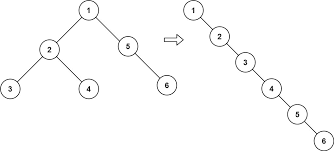
FLATTEN BINARY TREE
INTRODUCTION:
Flattening a binary tree involves rearranging its nodes to turn it into a flattened structure, typically a linked list. Instead of a hierarchical tree structure, the flattened tree represents a linear structure where all nodes are connected in a specific order, usually following a pre-order traversal pattern.
Process of Flattening a Binary Tree:
- Flatten to a Single List:
- The goal is to rearrange the tree nodes into a single list.
- Each node in the flattened structure should have its
leftpointer set toNone, and therightpointer should point to the next node in the flattened sequence.
- Preserving the Order:
- The order of nodes in the flattened structure typically follows a pre-order traversal.
- During flattening, the nodes are rearranged in a way that allows traversal in the pre-order sequence while maintaining the connections between nodes.
- Traversing the Tree:
- To flatten the tree, you'll likely use a recursive approach or an iterative method, traversing the tree and rearranging the nodes along the way to achieve the desired flattened structure.
- Utilizing Pointers:
- You'll manipulate pointers (
leftandright) to restructure the tree nodes into a flattened linked list. - As you traverse the tree, you'll adjust the pointers to create the flattened structure.
- You'll manipulate pointers (
OVERVEIW:
-
Restructuring Nodes:
- The primary goal is to rearrange the nodes in a way that preserves a specific sequence, usually following a pre-order traversal.
- Each node's
leftpointer is set toNone, and therightpointer establishes connections between nodes to create the flattened structure.
-
Traversal Techniques:
- Traversing the tree is crucial for rearranging the nodes. This traversal can be achieved using recursive or iterative methods like depth-first search (DFS) algorithms.
- As nodes are traversed, pointers are adjusted to restructure the tree into a flattened sequence.
-
Flattening Strategy:
- The flattening strategy might involve merging nodes, rearranging pointers, or creating a linked list-like structure that follows a specific order, typically pre-order traversal.
-
Preserving Node Relationships:
- While transforming the tree into a flattened structure, it's essential to maintain the relationships between nodes. The sequence should allow sequential traversal while retaining the original node
CODE:
# Python3 program to flatten a given Binary # Tree into linked list
class Node: def init(self, key): self.key = key self.left = None self.right = None
Utility function to create a new Node
def newNode(key): return Node(key)
Function to convert binary tree into linked list
def flatten(root): if root is None or (root.left is None and root.right is None): return
if root.left:
flatten(root.left)
tmpRight = root.right
root.right = root.left
root.left = None
t = root.right
while t.right:
t = t.right
t.right = tmpRight
flatten(root.right)
Inorder traversal
def inorder(root): if root: inorder(root.left) print(root.key, end=' ') inorder(root.right)
Driver code
if name == 'main': # Input the number of nodes in the binary tree n = int(input())
# Input the values of the nodes
# print("Enter the values of the nodes:")
nodes = [int(input()) for _ in range(n)]
# Build the binary tree
root = newNode(nodes[0])
index = 1
queue = [root]
while queue:
curr = queue.pop(0)
if index < n and nodes[index] is not None:
curr.left = newNode(nodes[index])
queue.append(curr.left)
index += 1
if index < n and nodes[index] is not None:
curr.right = newNode(nodes[index])
queue.append(curr.right)
index += 1
# Flatten the binary tree
flatten(root)
// print("The Inorder traversal after flattening binary tree: ", end='')
inorder(root)
# This code is contributed by pratham76
```
```java
import java.util.*;
class Node { int data; Node left, right;
Node(int key) {
data = key;
left = right = null;
}
}
class BinaryTree {
Node root;
// Function to convert binary tree into linked list by
// altering the right node and making left node NULL
public void flatten(Node node) {
// Base case - return if root is NULL
if (node == null)
return;
// Or if it is a leaf node
if (node.left == null && node.right == null)
return;
// If root.left children exists then we have to make
// it node.right (where node is root)
if (node.left != null) {
// Move left recursively
flatten(node.left);
// Store the node.right in Node named tempNode
Node tempNode = node.right;
node.right = node.left;
node.left = null;
// Find the position to insert the stored value
Node curr = node.right;
while (curr.right != null)
curr = curr.right;
// Insert the stored value
curr.right = tempNode;
}
// Now call the same function for node.right
flatten(node.right);
}
// Function for Inorder traversal
public void inOrder(Node node) {
// Base Condition
if (node == null)
return;
inOrder(node.left);
System.out.print(node.data + " ");
inOrder(node.right);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
BinaryTree tree = new BinaryTree();
// System.out.print("Enter the number of nodes: ");
int numNodes = scanner.nextInt();
// System.out.println("Enter the values of the nodes: ");
Node[] nodes = new Node[numNodes];
for (int i = 0; i < numNodes; i++) {
nodes[i] = new Node(scanner.nextInt());
}
tree.root = nodes[0];
for (int i = 0; i < numNodes; i++) {
if (2 * i + 1 < numNodes) {
nodes[i].left = nodes[2 * i + 1];
}
if (2 * i + 2 < numNodes) {
nodes[i].right = nodes[2 * i + 2];
}
}
// System.out.println("The Inorder traversal after flattening binary tree: ");
tree.flatten(tree.root);
tree.inOrder(tree.root);
}
}
```
```cpp
#include <iostream>
#include using namespace std;
struct Node { int key; Node *left, *right; };
Node* newNode(int key) { Node* node = new Node; node->key = key; node->left = node->right = NULL; return node; }
// Function to convert binary tree into linked list by // altering the right node and making left node point to // NULL void flatten(Node* root) { // base condition- return if root is NULL or if it is a // leaf node if (root == NULL || (root->left == NULL && root->right == NULL)) return; // if root->left exists then we have to make it // root->right if (root->left != NULL) { // move left recursively flatten(root->left); // store the node root->right Node* tmpRight = root->right; root->right = root->left; root->left = NULL; // find the position to insert the stored value Node* t = root->right; while (t->right != NULL) t = t->right; // insert the stored value t->right = tmpRight; } // now call the same function for root->right flatten(root->right); }
// To find the inorder traversal void inorder(Node* root) { // base condition if (root == NULL) return; inorder(root->left); cout << root->key << " "; inorder(root->right); }
/* Driver program to test above functions*/ int main() { int numNodes; // cout << "Enter the number of nodes: "; cin >> numNodes;
// Create nodes array
Node* nodes[numNodes];
// Input values for each node
// cout << "Enter the values of the nodes: ";
for (int i = 0; i < numNodes; ++i) {
int key;
cin >> key;
nodes[i] = newNode(key);
}
// Link nodes to form the binary tree
for (int i = 0; i < numNodes; ++i) {
if (2 * i + 1 < numNodes)
nodes[i]->left = nodes[2 * i + 1];
if (2 * i + 2 < numNodes)
nodes[i]->right = nodes[2 * i + 2];
}
// Flatten the binary tree
flatten(nodes[0]);
// cout << "The Inorder traversal after flattening binary tree: ";
inorder(nodes[0]);
return 0;
}
```
## TIME COMPLEXITY:
This time complexity arises from the need to visit and process each node in the tree once to restructure its pointers and create the flattened structure. The traversal operation scales linearly with the number of nodes in the tree, resulting in a time complexity of O(N) for the flattening process.
## SPACE COMPLEXITY:
- In a recursive approach, the space complexity is influenced by the function call stack and could reach O(N) in the worst-case scenario for unbalanced trees.
- In an iterative approach, the auxiliary data structures used for traversal might also consume O(N) space in the worst-case scenario.
- Therefore, the overall space complexity for flattening a binary tree could be O(N) in scenarios where additional space for traversal, either via recursion or iteration, grows with the number of nodes 'N' in the tree.
## **Applications:**
- Flattening a binary tree finds applications in optimizing algorithms that benefit from linear structures rather than hierarchical ones.
- It simplifies tree manipulation or navigation for specific tasks where a sequential processing approach is more suitable.
- The flattened structure can aid in efficient sequential access to tree nodes or facilitate specific data processing operations.
Test Cases
Test Case 1: Input: 6 1 2 5 3 4 6
Output: 1 2 3 4 5 6
Explanation:
In this test case, we input 6 nodes with values [1, 2, 5, 3, 4, 6].
The binary tree formed is:
1
/ \
2 5
/ \
3 6
\
4
After flattening the binary tree, the inorder traversal of the resulting linked list is 1 2 3 4 5 6.
Test Case 2: Input: 7 10 5 15 3 7 12 20
Output: 3 5 7 10 12 15 20
Explanation: In this test case, we input 7 nodes with values [10, 5, 15, 3, 7, 12, 20].
The binary tree formed is:
10
/ \
5 15
/ \ / \
3 7 12 20
After flattening the binary tree, the inorder traversal of the resulting linked list is 3 5 7 10 12 15 20.
