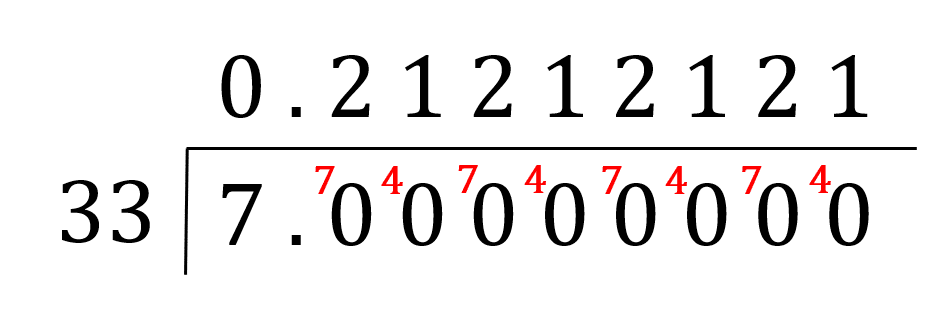
Fraction to Recurring Decimal

A fraction can be converted to a recurring decimal by dividing the numerator and denominator by a common factor. This process ensures that the decimal does not go on indefinitely.

Advantages :

They can represent ratios more accurately than decimals, they are useful in common measurements such as time and temperature, and they can be manipulated algebraically more easily.
Decimals and fractions allow for more precise calculations, especially when dealing with very small or very large numbers. Using percentages can lead to rounding errors and imprecise results.

Disadvantages :

fractions can be more difficult to work with when they have large numerators or denominators, they can be less intuitive than decimals for some people, and they require certain procedures to compare or add fractions that can be error-prone if not done carefully.

Code :

Python code :

def fraction_to_recurring_decimal(numerator, denominator): if numerator == 0: return "0"

result = []

# Handle the sign
if (numerator < 0) ^ (denominator < 0):
    result.append("-")

# Take the absolute values
numerator, denominator = abs(numerator), abs(denominator)

# Add the integer part
result.append(str(numerator // denominator))
remainder = numerator % denominator

if remainder == 0:
    return ''.join(result)

result.append(".")
seen_remainders = {}

while remainder != 0:
    if remainder in seen_remainders:
        # Recurring part found
        index = seen_remainders[remainder]
        result.insert(index, "(")
        result.append(")")
        break

    seen_remainders[remainder] = len(result)
    remainder *= 10
    result.append(str(remainder // denominator))
    remainder %= denominator

return ''.join(result)

if name == "main": numerator = int(input()) denominator = int(input())

result = fraction_to_recurring_decimal(numerator, denominator)

print(f"The recurring decimal representation is: {result}")

C++ code :

#include #include <unordered_map> #include

std::string fractionToDecimal(int numerator, int denominator) { if (numerator == 0) { return "0"; }

std::string result;

// Handle the sign
if ((numerator < 0) ^ (denominator < 0)) {
    result += "-";
}

// Take the absolute values
long long num = std::abs(static_cast<long long>(numerator));
long long den = std::abs(static_cast<long long>(denominator));

// Add the integer part
result += std::to_string(num / den);
long long remainder = num % den;

if (remainder == 0) {
    return result;
}

result += ".";

std::unordered_map<long long, int> seen_remainders;

while (remainder != 0) {
    if (seen_remainders.find(remainder) != seen_remainders.end()) {
        // Recurring part found
        result.insert(seen_remainders[remainder], 1, '(');
        result += ')';
        break;
    }

    seen_remainders[remainder] = result.length();
    remainder *= 10;
    result += std::to_string(remainder / den);
    remainder %= den;
}

return result;

}

int main() { int numerator, denominator;

std::cin >> numerator;

std::cin >> denominator;

std::string result = fractionToDecimal(numerator, denominator);

std::cout << result << std::endl;

return 0;

}

Java Code :

import java.util.HashMap; import java.util.Map; import java.util.Scanner;

public class FractionToDecimal {

public static String fractionToDecimal(int numerator, int denominator) {
    if (numerator == 0) {
        return "0";
    }

    StringBuilder result = new StringBuilder();

    // Handle the sign
    if ((numerator < 0) ^ (denominator < 0)) {
        result.append("-");
    }

    // Take the absolute values
    long num = Math.abs((long) numerator);
    long den = Math.abs((long) denominator);

    // Add the integer part
    result.append(num / den);
    long remainder = num % den;

    if (remainder == 0) {
        return result.toString();
    }

    result.append(".");

    Map<Long, Integer> seenRemainders = new HashMap<>();

    while (remainder != 0) {
        if (seenRemainders.containsKey(remainder)) {
            // Recurring part found
            int index = seenRemainders.get(remainder);
            result.insert(index, "(");
            result.append(")");
            break;
        }
        seenRemainders.put(remainder, result.length());
        remainder *= 10;
        result.append(remainder / den);
        remainder %= den;
    }

    return result.toString();
}

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);

    // Prompt the user to enter the numerator
    //   System.out.print("Enter the numerator: ");
    int numerator = scanner.nextInt();

    // Prompt the user to enter the denominator
    // System.out.print("Enter the denominator: ");
    int denominator = scanner.nextInt();

    // Calculate the fraction to decimal representation
    String result = fractionToDecimal(numerator, denominator);

    // Display the result
    System.out.println(result);

    scanner.close();
}

}

Time complexity :

The time complexity of converting a fraction to a recurring decimal is O(log n) where n is the denominator of the fraction. This is because the algorithm involves repeatedly dividing by the denominator until the remainder is less than 1. The number of iterations required is proportional to the number of digits in the numerator, which is at most log n.

Space complexity :

The space complexity of converting a fraction to recurring decimal is O(1). This is because the conversion involves either storing a fixed size integer representation of the fraction or using a floating point representation that requires a fixed amount of memory, regardless of the size of the input fraction. If you meant to ask about the space complexity of storing recurring decimal to fraction conversion formulas, it would be O(klogk) where k is the precision of the recurring decimal.

Test Cases

Input:
2
3
Output:
0.(6)

Explanation: The fraction 2/3 is a recurring decimal with "6" repeating infinitely. Hence, the result is "0.(6)".
Input:
4
5
Output:
0.8

Explanation: The fraction 4/5 results in a non-recurring decimal, "0.8".
Input:
1
2
Output:
0.5

Explanation: The fraction 1/2 results in a non-recurring decimal, "0.5".