LEVEL ORDER TRAVERSAL

Venkys.io

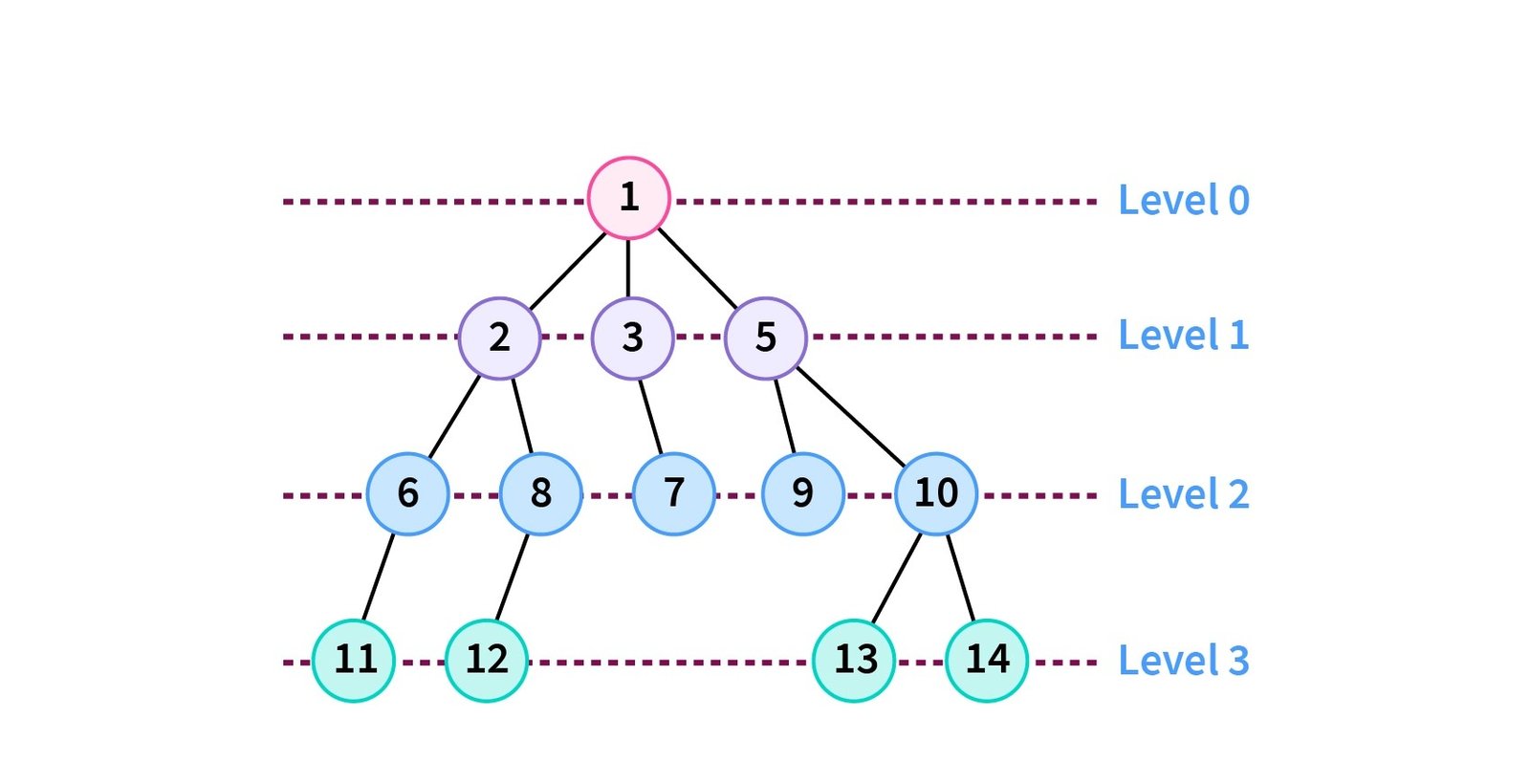
LEVEL ORDER TRAVERSAL

Level order traversal, also known as breadth-first traversal, is a fundamental technique in computer science and data structures used to explore and traverse trees, particularly binary trees and binary search trees. This method is also applicable to other data structures like graphs with slight modifications.

INTRODUCTION

Level order traversal involves visiting all the nodes in a tree or graph level by level, starting from the root or any other specified starting point. The key idea is to process all the nodes at a particular level before moving on to the next level. It's named "level order" because it explores the tree level by level, from top to bottom.

OVERVIEW OF LEVEL ORDER TRAVERSAL

Level order traversal is a fundamental tree traversal algorithm used to explore and visit all the nodes in a tree or graph in a systematic manner. This traversal method operates in a breadth-first fashion, meaning it starts at the root node (or another specified starting point) and systematically visits nodes level by level, moving from left to right within each level.

Here's an overview of level order traversal:

Initialization: The traversal begins by initializing a data structure called a queue, which is used to keep track of the nodes to be visited. The root node (or the starting node) is enqueued to the queue to kickstart the traversal.
Iterative Process: Level order traversal is typically implemented using a loop that continues until the queue is empty. The loop consists of the following key steps:

a. Dequeue: In each iteration of the loop, the algorithm dequeues (removes) a node from the front of the queue. This node is the one currently being processed.

b. Process Node: The dequeued node is processed, which could involve displaying its value, performing specific operations, or collecting data from the node.

c. Enqueue Children: If the dequeued node has children (e.g., left and right children in a binary tree), these children are enqueued into the queue. This ensures that the children are processed in the next iteration of the loop, preserving the level-order nature of the traversal.
Repeat Until Queue Is Empty: The loop continues until the queue becomes empty. This means that all nodes in the tree or graph have been visited in a level-order fashion.
Result: The result of a level order traversal can vary depending on the specific use case. In most cases, you would process the nodes (e.g., display their values), which could be used to print the tree, search for specific nodes, perform calculations, or solve various problems related to the data structure being traversed.

#copyrights to venkys.io
#for more programs visit venkys.io
#python program for level order traversal

#Time complexity:O(n)
#Space complexity:o(n)

#A node structure
class Node:
    def __init__(self, data):
        self.data = data
        self.left = self.right = None

# Function to print level order traversal of tree
def VSDlevelorder(root):
    queue = [root]
    while queue:
        node = queue.pop(0)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)
        print(node.data)

# Driver program to test above function
if __name__ == "__main__":
    # Taking input for the binary tree nodes from stdin
    root_data = int(input())
    root = Node(root_data)

    root.left = Node(int(input()))
    root.right = Node(int(input()))

    root.left.left = Node(int(input()))
    root.left.right = Node(int(input()))

    root.right.left = Node(int(input()))
    root.right.right = Node(int(input()))

    # Calling the function for level order traversal
    VSDlevelorder(root)

Step-by-Step Explanation

The node class defines a simple binary tree node with a constructor **init** that initializes the node with a given data value and sets both left and right child pointers to None.
The level order function performs a level order traversal of a binary tree.

It uses a queue to keep track of the nodes to be visited.
The traversal starts from the root node, and in each iteration, it dequeues a node, enqueues its left and right children if they exist, and prints the data of the dequeued node.

In this block, a binary tree is created by instantiating nodes and linking them appropriately.

Finally, the level order function is called with the root of the tree, which prints the level order traversal of the binary tree.

This code essentially demonstrates a basic implementation of a level order traversal algorithm for a binary tree using a queue data structure.

Test Case 1: Null Tree

Input:

Enter the value for the root node: 1

Test Case 2: True Binary Tree

Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7

Test Case 3: False Binary Tree

Input:

Explanation: This input creates an unbalanced binary tree. The output should be in the order 1,2,3,4,5,6,7,8 representing the level order traversal. This demonstrates that the code handles unbalanced trees as well.

Time and Space Complexity Analysis

Let's analyze the time and space complexity of the provided level order traversal code:

Time Complexity:

The time complexity is O(N), where N is the number of nodes in the binary tree. This is because each node is processed once, and in the worst case, every node is enqueued and dequeued once.

Space Complexity:

The space complexity is also O(N), where N is the number of nodes in the binary tree. In the worst case, when the tree is completely skewed and every level has only one node, the maximum number of nodes that can be present in the queue at any given time is N/2. Therefore, the space complexity is O(N) due to the queue used for the traversal.

In a balanced binary tree, the maximum number of nodes in the queue at any given time would be proportional to the maximum number of nodes in a level, which is O(2^(h-1)) for a binary tree of height h. In big-O notation, this is still O(N), where N is the total number of nodes in the tree.

//copyrights to venkys.io
// for more programs visit venkys.io
// java program for level order traversal

// Time complexity
// Space complexity 

// Importing necessary Java utility classes
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

// Definition of a Node in a binary tree
class Node {
    int data;
    Node left = null, right = null;

    // Constructor to initialize a Node with data
    Node(int data) {
        this.data = data;
    }
}

public class Main {

    // Function to perform level order traversal of a binary tree
    static void levelOrder(Node root) {
        Queue<Node> q = new LinkedList<>();

        // Create a queue to store nodes during traversal
        q.add(root);
        // Add the root node to the queue
        while (!q.isEmpty()) {
            Node node = q.poll();
            if (node.left != null)
                q.add(node.left);
            if (node.right != null)
                q.add(node.right);
            System.out.print(node.data + " ");
        }

    }

    // Main method to test the levelOrder function
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // System.out.println("Enter the value for the root node:");
        int rootValue = scanner.nextInt();
        Node root = new Node(rootValue);

        // System.out.println("Enter values for left and right children of the root node (0 if no child):");
        root.left = new Node(scanner.nextInt());
        root.right = new Node(scanner.nextInt());

        root.left.left = new Node(scanner.nextInt());
        root.left.right = new Node(scanner.nextInt());

        root.right.left = new Node(scanner.nextInt());
        root.right.right = new Node(scanner.nextInt());

        // Calling the levelOrder function to perform level order traversal
        // System.out.println("Level Order Traversal:");
        levelOrder(root);
    }
}

Test Case 1: Null Tree

Input:

Enter the value for the root node: 1 Enter values for left and right children of the root node (0 if no child): 0 0

Test Case 2: True Binary Tree

Input:

Enter the value for the root node: 1 Enter values for left and right children of the root node (0 if no child): 2 3 Enter values for left and right children of the left child: 4 5 Enter values for left and right children of the right child: 6 7

Explanation: This input creates a balanced binary tree. The output should be in the order

1 2 3 4 5 6 7 representing the level order traversal.

Test Case 3: False Binary Tree

Input:

Explanation: This input creates an unbalanced binary tree. The output should be in the order

1 2 3 4 5 6 7 8 representing the level order traversal. This demonstrates that the code handles unbalanced trees as well

Step-by-step Explanation

Node Class: This class defines a basic structure for a node in a binary tree. Each node has an integer data value, a reference to its left child (left), and a reference to its right child (right). The constructor Node(int data) initializes a node with the given data.
Main Class: This is the main class that contains the main method, which is the entry point for execution.
level Order Method: level order is a static method that performs a level-order traversal (Breadth-First Search) of a binary tree.

It takes the root of the tree as a parameter.
A queue (q) is used to keep track of the nodes during traversal.
The root node is added to the queue.
While the queue is not empty, it dequeues a node, processes it, and enqueues its left and right children (if they exist).
The data of each processed node is printed.

Main method: The main method is the entry point for the program.

It creates a sample binary tree by instantiating nodes and connecting them.
The level order method is called with the root of the tree, initiating the level-order traversal.

The program prints the data of each node in the binary tree in level-order.

In summary, the code defines a binary tree, implements a level-order traversal algorithm using a queue, creates a sample binary tree in the main method, and finally, executes the level-order traversal on the tree. The output demonstrates the order in which the nodes are visited during the traversal.

// copyrights to venkys.io
// for more programs visit venkys.io
// c++ program for levelordertraversal
#include <iostream>
#include <queue>

// Node class to represent a binary tree node
class Node {
public:
    int data;
    Node *left = nullptr;
    Node *right = nullptr;

    // Constructor to initialize a node with data
    Node(int val) {
        data = val;
    }
};

// Function to perform level order traversal of a binary tree
void levelOrder(Node *root) {
    std::queue<Node *> q;  // Create a queue to store nodes during traversal
    q.push(root);          // Enqueue the root node to start the traversal

    // Continue traversal until the queue is empty
    while (!q.empty()) {
        Node *node = q.front();
        q.pop();

        if (node->left)
            q.push(node->left);
        if (node->right)
            q.push(node->right);

        std::cout << node->data << " ";  // Print the data of the current node
    }
}

// Main function to test the levelOrder function
int main() {
    int rootData;
    // std::cout << "Enter the value for the root node: ";
    std::cin >> rootData;

    Node *root = new Node(rootData);

    // Taking input for the binary tree nodes from stdin
    // std::cout << "Enter the value for the left child of the root: ";
    int leftData;
    std::cin >> leftData;
    root->left = new Node(leftData);

    // std::cout << "Enter the value for the right child of the root: ";
    int rightData;
    std::cin >> rightData;
    root->right = new Node(rightData);

    // std::cout << "Enter the value for the left child of the left child: ";
    int leftLeftData;
    std::cin >> leftLeftData;
    root->left->left = new Node(leftLeftData);

    // std::cout << "Enter the value for the right child of the left child: ";
    int leftRightData;
    std::cin >> leftRightData;
    root->left->right = new Node(leftRightData);

    // std::cout << "Enter the value for the left child of the right child: ";
    int rightLeftData;
    std::cin >> rightLeftData;
    root->right->left = new Node(rightLeftData);

    // std::cout << "Enter the value for the right child of the right child: ";
    int rightRightData;
    std::cin >> rightRightData;
    root->right->right = new Node(rightRightData);

    // Calling the levelOrder function to perform level order traversal
    levelOrder(root);

    return 0;
}

Step-by-step explanation

Node Class: This class defines a basic structure for a node in a binary tree. Each node has an integer data value, a pointer to its left child (left), and a pointer to its right child (right). The constructor Node(int val ) initializes a node with the given data.
level Order Function: level order is a function that performs a level-order traversal (Breadth-First Search) of a binary tree. It takes the root of the tree as a parameter.

A (q) is used to keep track of the nodes during traversal.

The root node is enqueued into the queue.
While the queue is not empty, it dequeues a node, processes it, and enqueues its left and right children (if they exist).
The data of each processed node is printed.

Main Function: The main function is the entry point for the program. It creates a sample binary tree by dynamically allocating nodes and connecting them using pointers. The levelorder function is called with the root of the tree, initiating the level-order traversal.
The program prints the data of each node in the binary tree in level-order.

In summary, the C++ code is similar to the Java code you provided earlier. It defines a binary tree, implements a level-order traversal algorithm using a queue, creates a sample binary tree in the main function, and executes the level-order traversal on the tree. The output demonstrates the order in which the nodes are visited during the traversal.

Test Case 1: Null Tree

Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 0 Enter the value for the right child of the root: 0 Enter the value for the left child of the left child: 0 Enter the value for the right child of the left child: 0 Enter the value for the left child of the right child: 0 Enter the value for the right child of the right child: 0

Explanation: In this case, a tree with only the root node is created. The output should be 1 as there are no left or right children.

Test Case 2: True Binary Tree

Input:

Explanation: This input creates a balanced binary tree. The output should be in the order

1 2 3 4 5 6 7 representing the level order traversal.

Test Case 3: False Binary Tree

Input:

Explanation: This input creates an unbalanced binary tree. The output should be in the order

1 2 3 4 5 6 7 8 representing the level order traversal. This demonstrates that the code handles unbalanced trees as well.

Real-World Applications of level order traversal

Level order traversal of a binary tree is a fundamental algorithm that is widely used in various real-world applications. Here are some examples of how level order traversal is applied in different contexts:

Breadth-First Search (BFS) in Graphs:
- Level order traversal is essentially a BFS algorithm when applied to a graph represented as an adjacency matrix or list.
- BFS is used to find the shortest path between two nodes in an unweighted graph.
- It's also used in network routing protocols to explore neighboring nodes in a systematic manner.
Binary Tree Operations:
- Level order traversal is commonly used to perform operations on a binary tree level by level.
- It's useful for tasks like finding the height of a binary tree, checking if a binary tree is balanced, or constructing a binary tree from its level order traversal.
Print Tree in a Hierarchical Structure:
- Level order traversal allows for the printing of a binary tree in a hierarchical structure, making it easier to visualize and understand the tree's organization.
Finding the Deepest Node or Minimum Depth of a Binary Tree:
- Level order traversal can be used to find the deepest node in a binary tree or to calculate the minimum depth of the tree.
- Applications include decision trees in machine learning where determining the depth of a tree is crucial for understanding the model complexity.
Web Crawling and Indexing:
- In web crawling, level order traversal can be employed to systematically visit and index web pages.
- The traversal ensures that pages closer to the starting point (root) are processed before moving on to deeper levels.

These are just a few examples, and level order traversal serves as a foundational algorithm in various computer science and data structure applications. Its simplicity and efficiency make it a valuable tool in many problem-solving scenarios.