MaxHeapSort

Introduction to MaxHeapSort

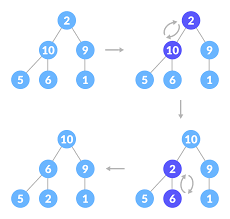
MaxHeapSort is a sorting algorithm that operates on a data structure called a max heap. It is an efficient algorithm for sorting elements in ascending order. In MaxHeapSort, the largest element is repeatedly extracted from the max heap and placed at the end of the sorted array. The heap is then restructured to maintain the heap property, and the process is repeated until all elements are sorted.

MaxHeapSort has a time complexity of O(n log n), making it suitable for sorting large datasets. It is commonly used in various applications where sorting is required.

Overview of MaxHeapSort

MaxHeapSort is a sorting algorithm that operates on a data structure called a max heap. It is known for its efficiency in sorting elements in ascending order. The algorithm repeatedly extracts the largest element from the max heap and places it at the end of the sorted array. This process continues until all elements are sorted. MaxHeapSort has a time complexity of O(n log n), making it a suitable choice for sorting large datasets. It is widely used in various applications that require sorting.

Code(Python):


""" Copyrights to venkys.io
For more information, visit https://venkys.io """

# Python program for performing Breadth First Search

# Space complexity: O(log n)
# Time complexity: O(n log n) 

# Function to maintain max heap properties
def VSDmaxHeapify(arr,size,i):

    #declare current element index is largest element
    large=i 
    #find index of left child
    leftchild=(2*i)+1 
    #find index of right child
    rightchild=(2*i)+2 
    # check largest element between left child and current element
    if leftchild<size and arr[i]<arr[leftchild]:
        large=leftchild
 
    # check largest element between right child and large element
    if rightchild<size and arr[large]<arr[rightchild]:
        large=rightchild
    
    # if large element is not current element 
    # swap current element with large element 
    # heapify the the current array
    if large!=i:
        arr[large],arr[i]=arr[i],arr[large]
        VSDmaxHeapify(arr,size,large)

# Function to maintain max heap properties
def VSDminHeapify(arr,size,i):
    
    #Declare the current element index as smallest
    small=i

    #Find the index of leftchild element
    leftchild=(2*i)+1

    #Find the index of rightchild element
    rightchild=(2*i)+2

    #Check the smallest element between leftchild and current element
    if leftchild<size and arr[i]>arr[leftchild]:
        small=leftchild
    
    #Check the smallest element between rightchild and smallest element
    if rightchild<size and arr[small]>arr[rightchild]:
        small=rightchild
    
    # If smallest element is not current element
    # Swap the smallest element and current element
    # Heapify the current array
    if small!=i:
        arr[small],arr[i]=arr[i],arr[small]
        VSDminHeapify(arr,size,small)

# Function to insert elements into max heap
def insert(array,num):
    if len(array)==0:
        array.append(num)
    else:
        array.append(num)
        for i in range(len(array)):
            VSDmaxHeapify(array,len(array),i)

# Function to sort the given array using maxheap in ascending order
def VSDMaxheapsort(array):
    size=len(array)

    # Heapify the given array into maxheap
    for i in range((size//2)-1,-1,-1):
        VSDmaxHeapify(array,size,i)

    # Find the max element in array
    # Swap the max element with last index element 
    # Decrease the last index by 1
    # Heapify the current array upto last index
    for i in range(size-1,0,-1):
        array[i],array[0]=array[0],array[i]
        VSDmaxHeapify(array,i,0)
  

# Function to sort the given array using minheap in descending order
def VSDMinheapsort(array):
    size=len(array)

    # Heapify the given array into min heap
    for i in range((size//2)-1,-1,-1):
        VSDminHeapify(array,size,i)
    
    # Find the min element in array
    # Swap the min element with last index element
    # Decrease the last index by 1
    # Heapify the current array upto last index
    for i in range(size-1,-1,-1):
        array[0],array[i]=array[i],array[0]
        VSDminHeapify(array,i,0)

#Fucntion to print array
def printarray(array):

    for i in array:
        print(i,end=" ")
    print()

if __name__ == "__main__":
    # Taking input for the array from the user
    input_str = input("Enter the array elements separated by space: ")
    arr = list(map(int, input_str.split()))

    print("Original array:")
    printarray(arr)

    # Sorting using max heap
    print("Sorted array using maxheapsort:")
    VSDMaxheapsort(arr)
    printarray(arr)

    # Sorting using min heap
    print("Sorted array using minheapsort:")
    VSDMinheapsort(arr)
    printarray(arr)

Step-by-step Explaination:

The code provided demonstrates the implementation of the MaxHeapSort algorithm in Python. Here is a step-by-step explanation of how the algorithm works:

The VSDmaxHeapify function is defined to maintain the max heap properties. It takes three parameters: the array, the size of the heap, and the index of the current element.
The VSDminHeapify function is defined to maintain the min heap properties. It takes the same parameters as VSDmaxHeapify.
The insert function is defined to insert elements into the max heap. It takes the array and the number to be inserted as parameters.
The VSDMaxheapsort function is defined to sort the given array using the max heap. It first heapifies the array into a max heap. Then, it repeatedly swaps the maximum element with the last element in the array, reduces the size of the array by 1, and heapifies the remaining array.
The VSDMinheapsort function is defined to sort the given array using the min heap. It follows a similar process as VSDMaxheapsort, but maintains the min heap properties instead.
The printarray function is defined to print the elements of an array.
In the main program, an example array arr is created with some random elements.
The VSDMaxheapsort function is called to sort the array in ascending order using the max heap.
The sorted array is printed using the printarray function.
The VSDMinheapsort function is called to sort the array in descending order using the min heap.
The sorted array is printed again.

This is a basic overview of how the MaxHeapSort algorithm works. The provided code demonstrates the implementation and usage of the algorithm in Python.

Code(Java):


/* Copyrights to venkys.io
For more information, visit https://venkys.io */

// Space complexity: O(log n)
// Time complexity: O(n log n)
import java.util.Scanner;

public class maxsort {
    // Class to hold the structure of a node in a tree
    public static class Node {
        int data; // Holds the value of the node
        Node left; // Holds the left pointer of the node
        Node right; // Holds the right pointer of the node

        // Default constructor
        Node(int data) {
            this.data = data;
            this.left = this.right = null;
        }
    }

    // Root node
    public static Node root = null;

    // Variable to hold the count of left nodes
    public static int leftcount = 0;

    // Variable to hold the count of right nodes
    public static int rightcount = 0;

    // Variable to maintain the count of nodes in the heap for appropriate deletion
    public static int deletecount = 0;

    // Variable to hold the appropriate child node for deletion
    public static Node deletenode = null;

    // Variable to hold the parent of the child to be deleted
    public static Node parent = null;

    // Method to Build Heap along with maintenance of a complete binary tree
    public static Node VSDbuildHeap(Node root, Node newNode) {
        if (root == null)
            root = newNode; // Null check
        else if (root.left != null && root.right != null) // Checking whether both left and right children are present
                                                            // for the root
        {
            leftcount = VSDsubtreeCount(root.left); // Getting left nodes count from the left of the current root
            rightcount = VSDsubtreeCount(root.right); // Getting right nodes count from the right of the current root

            int height = VSDfindHeight(root); // Getting the height of the tree
            // Checking for the correct position to insert
            if (leftcount < (VSDexpectedCount(height) / 2)) {
                VSDbuildHeap(root.left, newNode);
            } else if (leftcount == rightcount)
                VSDbuildHeap(root.left, newNode);
            else
                VSDbuildHeap(root.right, newNode);
        } else if (root.left == null) {
            root.left = newNode;

        } else if (root.right == null) {
            root.right = newNode;

        }

        return root;
    }

    // Function to maintain max heap properties
    public static Node VSDHeapify(Node current) {
        if (current.left != null)
            current.left = VSDHeapify(current.left);
        if (current.right != null)
            current.right = VSDHeapify(current.right);
        if (current.left != null && current.left.data > current.data) {
            int temp = current.left.data;
            current.left.data = current.data;
            current.data = temp;

        }
        if (current.right != null && current.right.data > current.data) {
            int temp = current.right.data;
            current.right.data = current.data;
            current.data = temp;
        }
        return current;
    }

    // Function to return the expected node count for a given height
    public static int VSDexpectedCount(int h) {
        int count = 0;
        while (h >= 0) {
            count += Math.pow(2, h);
            h--;
        }
        return count;
    }

    // Function to return the node count for a given subtree
    public static int VSDsubtreeCount(Node current) {
        int leftheight = 0; // variable to hold the height of the left subtree
        int rightheight = 0; // variable to hold the height of the right subtree
        // Traversing to the left subtree to find the max height
        if (current.left != null) {
            leftheight = VSDsubtreeCount(current.left);
        }
        // Traversing to the right subtree to find the max height
        if (current.right != null) {
            rightheight = VSDsubtreeCount(current.right);
        }
        // Selecting the maximum height and adding 1 for root's height
        int count = rightheight + leftheight + 1;
        return count;
    }

    // Function to return the height of the tree
    public static int VSDfindHeight(Node current) {
        if (current == null)
            return -1;
        else {
            int lh = VSDfindHeight(current.left);
            int rh = VSDfindHeight(current.right);

            if (lh > rh)
                return (lh + 1);
            else
                return (rh + 1);
        }
    }

    // Function to display elements in max heap using inorder traversal
    public static void VSDinorder(Node root) {
        if (root.left != null)
            VSDinorder(root.left);
        System.out.println(root.data);
        if (root.right != null)
            VSDinorder(root.right);
    }

    /* Function to choose the most recently inserted element based on count */
    public static void VSDchooseNode(Node current, int level, int size) {
        if (current == null) {
            return;
        }
        if (level == 0) {
            deletecount++;
            if (deletecount == size / 2) {
                parent = current;
            }
            if (deletecount == size) {
                deletenode = current;
                return;
            }
        } else if (level > 0) {

            VSDchooseNode(current.left, level - 1, size);
            VSDchooseNode(current.right, level - 1, size);
        }

    }

    // Function to delete the root node from the heap
    public static Node VSDdeleteNode(Node root, int height, int size) {
        // Obtain the correct child node to replace with the root
        for (int i = 0; i <= height; i++) {
            VSDchooseNode(root, i, size);
        }
        int temp = root.data;
        root.data = deletenode.data;
        deletenode.data = temp;
        // Deleting the node
        if (parent.right != null)
            parent.right = null;
        else
            parent.left = null;
        // calling heapify to maintain max heap properties
        root = VSDHeapify(root);
        return root;
    }

    public static void main(String args[]) {
        Scanner scanner = new Scanner(System.in);

        System.out.println("Enter the number of elements in the heap:");
        int size = scanner.nextInt();

        int[] arr = new int[size];
        System.out.println("Enter the elements separated by space:");
        for (int i = 0; i < size; i++) {
            arr[i] = scanner.nextInt();
        }

        Node n;
        root = null;
        for (int i = 0; i < arr.length; i++) {
            n = new Node(arr[i]);
            root = VSDbuildHeap(root, n);
            root = VSDHeapify(root); // Calling function to maintain max heap properties
        }

        System.out.println("Insertion");
        VSDinorder(root);

        System.out.println("The descending order is:");
        while (size > 1) {
            deletecount = 0;
            System.out.println(root.data);
            int height = VSDfindHeight(root);
            root = VSDdeleteNode(root, height, size);
            size--;
        }
        System.out.println(root.data);

        scanner.close();
    }
}

step-by-step Explaination:

The VSDMaxHeapSort class contains the main method and other helper methods.
The Node class represents a node in the binary tree. It has three fields: data (holds the value of the node), left (holds the left pointer of the node), and right (holds the right pointer of the node).
The VSDbuildHeap method is used to build the max heap from the given array of integers. It recursively inserts nodes into the tree based on the heap property.
The VSDHeapify method is used to maintain the max heap property by comparing the node with its children and swapping if necessary.
The VSDexpectedCount method calculates the expected number of nodes for a given height in a complete binary tree.
The VSDsubtreeCount method calculates the number of nodes in a subtree rooted at a given node.
The VSDfindHeight method calculates the height of the tree.
The VSDinorder method performs an inorder traversal of the tree and prints the elements in the max heap.
The VSDchooseNode method selects the most recently inserted element based on the count.
The VSDdeleteNode method deletes the root node from the heap and replaces it with the appropriate child node.
The main method creates an array of integers, builds the max heap, and then performs the heap sort by deleting the root node iteratively.

Code(CPP):


/* Copyrights to venkys.io
For more information, visit https://venkys.io */

// Space complexity: O(log n)
// Time complexity: O(n log n)

#include<iostream>
using namespace std;

void swap(int arr[], int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void printarray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
}

void VSDmaxheapify(int arr[], int n, int i) {
    int large = i;
    int leftchild = (2 * i) + 1;
    int rightchild = (2 * i) + 2;

    if (leftchild < n && arr[i] < arr[leftchild])
        large = leftchild;
    if (rightchild < n && arr[large] < arr[rightchild])
        large = rightchild;
    if (large != i) {
        swap(arr, i, large);
        VSDmaxheapify(arr, n, large);
    }
}

void VSDminheapify(int arr[], int n, int i) {
    int small = i;
    int leftchild = (2 * i) + 1;
    int rightchild = (2 * i) + 2;

    if (leftchild < n && arr[i] > arr[leftchild]) {
        small = leftchild;
    }
    if (rightchild < n && arr[small] > arr[rightchild]) {
        small = rightchild;
    }
    if (small != i) {
        swap(arr, small, i);
        VSDminheapify(arr, n, small);
    }
}

void VSDMaxheapsort(int arr[], int n) {
    for (int i = (n / 2) - 1; i >= 0; i--) {
        VSDmaxheapify(arr, n, i);
    }
    for (int i = n - 1; i > 0; i--) {
        swap(arr, i, 0);
        VSDmaxheapify(arr, i, 0);
    }
}

void VSDMinheapsort(int arr[], int n) {
    for (int i = (n / 2) - 1; i >= 0; i--) {
        VSDminheapify(arr, n, i);
    }
    for (int i = n - 1; i > 0; i--) {
        swap(arr, i, 0);
        VSDminheapify(arr, i, 0);
    }
}

int main() {
    int n;

    cout << "Enter the number of elements: ";
    cin >> n;

    int arr[n];
    cout << "Enter the elements separated by space: ";
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }

    VSDMaxheapsort(arr, n);
    cout << "Sorted array using max heap sort: ";
    printarray(arr, n);

    VSDMinheapsort(arr, n);
    cout << "Sorted array using min heap sort: ";
    printarray(arr, n);

    return 0;
}

step-by-step Explaination:

The code provided consists of several functions and a main function. Here is a breakdown of the code structure:

swap: This function takes an array and two indices as input and swaps the elements at those indices.
printarray: This function takes an array and its size as input and prints the elements of the array.
VSDmaxheapify: This function takes an array, its size, and an index as input. It performs Max Heapify on the subtree rooted at the given index.
VSDminheapify: This function takes an array, its size, and an index as input. It performs Min Heapify on the subtree rooted at the given index.
VSDMaxheapsort: This function takes an array and its size as input. It builds a Max Heap from the array and performs Heap Sort to sort the array in ascending order.
VSDMinheapsort: This function takes an array and its size as input. It builds a Min Heap from the array and performs Heap Sort to sort the array in descending order.
main: The main function initializes an array with some values, calculates the size of the array, calls the VSDMaxheapsort function to sort the array in ascending order, prints the sorted array, calls the VSDMinheapsort function to sort the array in descending order, and prints the sorted array again.

Time Complexity Analysis:

The time complexity of the MaxHeapSort algorithm is determined by the two main operations: building the max heap and performing heapify during the sorting process.

Building the max heap: The VSDMaxheapsort function calls VSDmaxheapify for each non-leaf node in the heap. The VSDmaxheapify operation has a time complexity of O(log n), where n is the number of elements in the heap. Since there are n/2 non-leaf nodes in a heap, the time complexity of building the max heap is O(n).
Heapify during sorting: The second part of the algorithm involves repeatedly swapping the maximum element with the last element in the array and performing heapify on the remaining elements. This process is repeated n times, where n is the number of elements in the array. The heapify operation has a time complexity of O(log n). Therefore, the time complexity of heapify during sorting is O(n log n).

Overall, the time complexity of the MaxHeapSort algorithm is O(n + n log n), which simplifies to O(n log n) in the worst case.

Space Complexity Analysis:

The space complexity of the MaxHeapSort algorithm is determined by the auxiliary space used during the heapify operation.

Building the max heap: The space complexity of building the max heap is O(1) because it does not require any additional space.
Heapify during sorting: The space complexity of heapify during sorting is O(log n) because it uses the call stack to store the recursive function calls.

Therefore, the overall space complexity of the MaxHeapSort algorithm is O(log n).

It is important to note that the space complexity does not include the space required to store the input and output arrays.

This is the time and space complexity analysis of the MaxHeapSort algorithm.

Real World Applications of MaxHeapSort:

MaxHeapSort, also known as Heap Sort, is a versatile algorithm that finds applications in various domains. Here are some real-world applications where MaxHeapSort is commonly used:

Sorting: The primary application of MaxHeapSort is for sorting elements in an array or a data structure. It efficiently sorts elements in ascending or descending order, making it suitable for applications that require sorting large datasets.
Priority Queues: MaxHeapSort is used to implement priority queues, where elements with higher priority are dequeued first. The heap data structure, based on MaxHeapSort, efficiently supports insertion, deletion, and retrieval operations in priority queues.
Operating Systems: MaxHeapSort is utilized in operating systems for scheduling processes based on priority levels. It helps determine the order in which processes should be executed, allowing for efficient resource allocation and management.
Graph Algorithms: MaxHeapSort plays a crucial role in various graph algorithms, such as Dijkstra's algorithm for finding the shortest path in a graph. It assists in selecting the next vertex with the highest priority during graph traversal.
Event Scheduling: MaxHeapSort is employed in event-driven systems, where events have different priorities based on their significance or urgency. It ensures that events are processed in the correct order based on their priority levels.
Simulation and Gaming: MaxHeapSort is useful in simulation and gaming scenarios, such as real-time strategy games or simulations that require efficient sorting of game entities or events based on their priorities.

These are just a few examples of the real-world applications of MaxHeapSort. The algorithm's ability to efficiently handle priority-based operations and sort data makes it a valuable tool in various domains.