Max-Heap using CRUD operations
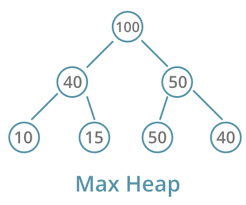
Exploring Max-Heap using CRUD operations :
Introduction to Heaps:
Heaps are a fundamental data structure used in computer science for efficient implementation of priority queues and various graph algorithms. A heap is a specialized tree-based structure that satisfies the heap property.
A binary heap is a complete binary tree where every parent node has a value greater than or equal to its children. This structure allows for quick retrieval and removal of the maximum element, making it an ideal choice for priority queue implementations.
Introduction to Max-Heap CRUD Operations:
In the context of heaps, CRUD operations refer to Create, Read, Update, and Delete. Max-Heap CRUD operations involve manipulating a max heap, ensuring that it maintains the heap property at all times.
Let's dive into each CRUD operation:
Overview of Max-Heap CRUD Operations:
-
Create (Insertion):
- Description: Adds a new element to the max heap while maintaining the heap property.
- Implementation: The new element is appended to the end of the heap, and then the
percolate_upmethod is called to ensure that the heap property is restored.
-
Read (Get Maximum):
- Description: Returns the maximum element in the max heap, which is always the root.
- Implementation: Simply retrieves the element at the root of the heap.
-
Update (Modify Element):
- Description: Updates an existing value in the max heap while preserving the heap property.
- Implementation: Finds the index of the old value, updates it with the new value, and then calls
percolate_upandmax_heapifyto maintain the heap property.
-
Delete (Remove Maximum):
- Description: Removes the maximum element (root) from the max heap while maintaining the heap property.
- Implementation: Replaces the root with the last element, pops the last element, and then calls
max_heapifyto reorder the heap.
These CRUD operations provide a comprehensive set of functionalities for working with a max heap. They ensure that the heap property is consistently upheld, allowing for efficient management of data in various applications.
PYTHON
code
# Copyrights to venkys.io
# For more information, visit https://venkys.io
# python program for Max-Heap CRUD
# Stable: Yes
# Inplace: Yes
# Adaptive: Yes
# Space complexity:O(n)
# Time complexity:
# Insertion: O(log N)
# Get Max: O(1)
# Update: O(log N)
# Delete Max: O(log N)
class MaxHeap:
def __init__(self):
# Initialize an empty list to represent the heap
self.heap = []
def percolate_up(self, index):
# Move the element up the heap until the heap property is restored
while index > 0:
parent = (index - 1) // 2
if self.heap[parent] >= self.heap[index]:
break
# Swap the current element with its parent
self.heap[parent], self.heap[index] = self.heap[index], self.heap[parent]
index = parent
def max_heapify(self, index):
# Ensure the heap property is maintained starting from the given index
left = 2 * index + 1
right = 2 * index + 2
largest = index
# Check if the left child is larger than the current largest element
if left < len(self.heap) and self.heap[left] > self.heap[largest]:
largest = left
# Check if the right child is larger than the current largest element
if right < len(self.heap) and self.heap[right] > self.heap[largest]:
largest = right
# If the largest element is not the current index, swap and continue heapifying
if largest != index:
self.heap[largest], self.heap[index] = self.heap[index], self.heap[largest]
self.max_heapify(largest)
def insert(self, val):
# Add a new element to the heap and percolate it up to maintain the heap property
self.heap.append(val)
self.percolate_up(len(self.heap) - 1)
def get_max(self):
# Return the maximum element in the heap (root of the heap)
if len(self.heap) == 0:
raise Exception("Heap is empty")
return self.heap[0]
def update(self, old_val, new_val):
try:
# Find the index of the old value in the heap
index = self.heap.index(old_val)
# Update the value, percolate up, and max heapify to maintain the heap property
self.heap[index] = new_val
self.percolate_up(index)
self.max_heapify(index)
except ValueError:
print("Value not in heap")
def delete_max(self):
if len(self.heap) == 0:
raise Exception("Heap is empty")
# Replace the root with the last element, pop the last element, and max heapify
self.heap[0] = self.heap.pop()
self.max_heapify(0)
def print_heap(self):
# Print all values in the heap
print(" ".join(map(str, self.heap)))
def main():
# Initialize max heap
heap = MaxHeap()
# Insert elements into heap
heap.insert(12)
heap.insert(10)
heap.insert(-10)
heap.insert(100)
# Print all values in heap
heap.print_heap()
# Get max value in heap
print("Max Value:", heap.get_max())
# Update value in heap
heap.update(12, 5)
print("Max Value after update:", heap.get_max())
# Delete max value from heap
heap.delete_max()
print("Max Value after deletion:", heap.get_max())
# Print all values in heap after deletion
heap.print_heap()
Code Explanation
The provided code implements a MaxHeap class in Python, allowing users to perform CRUD operations (Create, Read, Update, Delete) on a max heap data structure. Let's break down the code and provide a clear explanation:
Step 1 - Initialization:
self.heap = []
The MaxHeap class is initialized with an empty list, self.heap, which will store the elements of the max heap.
Step 2 - Percolate Up:
def percolate_up(self, index):
The percolate_up method is used during insertion to move a newly added element up the heap until the heap property is restored. It compares the element with its parent and swaps them if needed.
Step 3 - Max Heapify:
def max_heapify(self, index):
The max_heapify method is used to maintain the heap property from a given index. It compares the element with its left and right children, swaps with the largest child if needed, and recursively continues the process.
Step 4 - Insertion:
def insert(self, val):
The insert method adds a new element to the heap and then calls percolate_up to ensure the heap property is maintained.
Step 5 - Get Max:
def get_max(self):
The get_max method returns the maximum element in the heap, which is the root.
Step 6 - Update:
def update(self, old_val, new_val):
The update method updates an existing value in the heap. It finds the index, updates the value, and then calls percolate_up and max_heapify to maintain the heap property.
Step 7 - Delete Max:
def delete_max(self):
The delete_max method removes the maximum element (root) from the heap. It replaces the root with the last element, pops the last element, and then calls max_heapify to reorder the heap.
Step 8 - Print Heap:
def print_heap(self):
The print_heap method prints all values in the heap.
Step 9 - Main Function:
def main():
# Initialize max heap
heap = MaxHeap()
The main function demonstrates the usage of the MaxHeap class by initializing a heap, performing insertions, updates, deletions, and printing the heap at different stages.
This implementation provides a clear and organized way to work with Max-Heaps in Python.
C++
code
/* Copyrights to venkys.io
For more information, visit https://venkys.io */
// C++ program for Max_Heap CRUD
// Stable: No
// Inplace: Yes
// Adaptive: No
// Space complexity: O(N)
// Time complexity:
// Insertion: O(log N)
// Get Max: O(1)
// Update: O(log N)
// Delete Max: O(log N)
#include <iostream>
#include <vector>
#include <algorithm>
class MaxHeap {
private:
std::vector<int> heap;
// Move the element up the heap until the heap property is restored
void percolateUp(int index) {
while (index > 0) {
int parent = (index - 1) / 2;
if (heap[parent] >= heap[index]) {
break;
}
std::swap(heap[parent], heap[index]);
index = parent;
}
}
// Ensure the heap property is maintained starting from the given index
void maxHeapify(int index) {
int left = 2 * index + 1;
int right = 2 * index + 2;
int largest = index;
// Check if the left child is larger than the current largest element
if (left < heap.size() && heap[left] > heap[largest]) {
largest = left;
}
// Check if the right child is larger than the current largest element
if (right < heap.size() && heap[right] > heap[largest]) {
largest = right;
}
// If the largest element is not the current index, swap and continue heapifying
if (largest != index) {
std::swap(heap[largest], heap[index]);
maxHeapify(largest);
}
}
public:
// Add a new element to the heap and percolate it up to maintain the heap property
void insert(int val) {
heap.push_back(val);
percolateUp(heap.size() - 1);
}
// Return the maximum element in the heap (root of the heap)
int getMax() {
if (heap.size() == 0) {
throw "Heap is empty";
}
return heap[0];
}
// Update the value, percolate up, and max heapify to maintain the heap property
void update(int old_val, int new_val) {
auto it = std::find(heap.begin(), heap.end(), old_val);
if (it != heap.end()) {
*it = new_val;
percolateUp(it - heap.begin());
maxHeapify(it - heap.begin());
} else {
std::cout << "Value not in heap" << std::endl;
}
}
// Replace the root with the last element, pop the last element, and max heapify
void deleteMax() {
if (heap.size() == 0) {
throw "Heap is empty";
}
heap[0] = heap.back();
heap.pop_back();
maxHeapify(0);
}
// Print all values in the heap
void printHeap() {
for (int i : heap) {
std::cout << i << " ";
}
std::cout << std::endl;
}
};
int main() {
// Example usage of the MaxHeap class
MaxHeap heap;
heap.insert(12);
heap.insert(10);
heap.insert(-10);
heap.insert(100);
std::cout << "All values in heap: ";
heap.printHeap();
std::cout << "Max Value: " << heap.getMax() << std::endl;
heap.update(12, 5);
std::cout << "Max Value after update: " << heap.getMax() << std::endl;
heap.deleteMax();
std::cout << "Max Value after deletion: " << heap.getMax() << std::endl;
std::cout << "All values in heap: ";
heap.printHeap();
return 0;
}
java
code
/* Copyrights to venkys.io
For more information, visit https://venkys.io */
// java program for Max-Heap CRUD
// Stable: No
// Inplace: Yes
// Adaptive: No
// Space complexity: O(N)
// Time complexity:
// Insertion: O(log N)
// Get Max: O(1)
// Update: O(log N)
// Delete Max: O(log N)
import java.util.ArrayList;
import java.util.List;
// Class representing a max heap with CRUD operations
class MaxHeapCRUD {
private List<Integer> heap;
// Constructor initializes an empty list for the heap
public MaxHeapCRUD() {
this.heap = new ArrayList<>();
}
// Move the element up the heap until the heap property is restored
private void percolateUp(int index) {
while (index > 0) {
int parent = (index - 1) / 2;
if (heap.get(parent) >= heap.get(index)) {
break;
}
// Swap the current element with its parent
int temp = heap.get(parent);
heap.set(parent, heap.get(index));
heap.set(index, temp);
index = parent;
}
}
// Ensure the heap property is maintained starting from the given index
private void maxHeapify(int index) {
int left = 2 * index + 1;
int right = 2 * index + 2;
int largest = index;
// Check if the left child is larger than the current largest element
if (left < heap.size() && heap.get(left) > heap.get(largest)) {
largest = left;
}
// Check if the right child is larger than the current largest element
if (right < heap.size() && heap.get(right) > heap.get(largest)) {
largest = right;
}
// If the largest element is not the current index, swap and continue heapifying
if (largest != index) {
int temp = heap.get(largest);
heap.set(largest, heap.get(index));
heap.set(index, temp);
maxHeapify(largest);
}
}
// Add a new element to the heap and percolate it up to maintain the heap property
public void insert(int val) {
heap.add(val);
percolateUp(heap.size() - 1);
}
// Return the maximum element in the heap (root of the heap)
public int getMax() {
if (heap.size() == 0) {
throw new RuntimeException("Heap is empty");
}
return heap.get(0);
}
// Update the value, percolate up, and max heapify to maintain the heap property
public void update(int oldVal, int newVal) {
int index = heap.indexOf(oldVal);
if (index != -1) {
heap.set(index, newVal);
percolateUp(index);
maxHeapify(index);
} else {
System.out.println("Value not in heap");
}
}
// Replace the root with the last element, pop the last element, and max heapify
public void deleteMax() {
if (heap.size() == 0) {
throw new RuntimeException("Heap is empty");
}
heap.set(0, heap.remove(heap.size() - 1));
maxHeapify(0);
}
// Print all values in the heap
public void printHeap() {
for (int i : heap) {
System.out.print(i + " ");
}
System.out.println();
}
// Main method demonstrating usage of the MaxHeapCRUD class
public static void main(String[] args) {
MaxHeapCRUD heap = new MaxHeapCRUD();
heap.insert(12);
heap.insert(10);
heap.insert(52);
heap.insert(100);
heap.insert(50);
System.out.print("All values in heap: ");
heap.printHeap();
System.out.println("Max Value: " + heap.getMax());
heap.update(12, 5);
System.out.println("Max Value after update: " + heap.getMax());
heap.deleteMax();
System.out.println("Max Value after deletion: " + heap.getMax());
System.out.print("All values in heap: ");
heap.printHeap();
}
}
Code Explanation
Step by step explanation for Java and C++ :
-
Class Definition (MaxHeap):
- The code defines a class named
MaxHeaprepresenting a Max Heap data structure. - Private member for c++:
std::vector<int> heapis used to store the elements of the heap. -It uses a private list (heap) to store the elements of the heap in java. - The class has a constructor in java (MaxHeapCRUD()) that initializes an empty list for the heap.
- The code defines a class named
-
percolateUp Function:
- Private method
percolateUpmoves an element up the heap until the heap property is restored. - It takes an index as a parameter and swaps the element with its parent until the heap property is satisfied.
- Private method
-
maxHeapify Function:
- Private method
maxHeapifyensures the heap property is maintained starting from a given index. - It compares the element with its left and right children, swapping it with the largest child if needed.
- Private method
-
insert Function:
- Public method
insertadds a new element to the heap and ensures the heap property by callingpercolateUp.
- Public method
-
getMax Function:
- Public method
getMaxreturns the maximum element in the heap (the root).
- Public method
-
update Function:
- Public method
updateupdates a specified element in the heap with a new value. - It uses
std::findto locate the element, updates it, and then callspercolateUpandmaxHeapifyto maintain the heap property.
- Public method
-
deleteMax Function:
- Public method
deleteMaxremoves the maximum element (root) from the heap. - It replaces the root with the last element, pops the last element, and calls
maxHeapifyto restore the heap property.
- Public method
-
printHeap Function:
- Public method
printHeapprints all values in the heap.
- Public method
-
main Function:
- In the
mainfunction:- An instance of
MaxHeapnamedheapis created in c++.An instance of MaxHeapCRUD named heap is created in java - Elements (12, 10, -10, 100,50) are inserted into the heap using
insert. - All values in the heap are printed using
printHeap. - The maximum value in the heap is printed using
getMax. - An update is performed, changing the value 12 to 5 using
update. - The maximum value after the update is printed.
- The maximum element is deleted using
deleteMax. - The maximum value after deletion is printed.
- Finally, all values in the heap after deletion are printed.
- An instance of
- In the
This code demonstrates the basic operations (insertion, update, deletion) on a Max Heap.
Time and Space Complexity Analysis:
Time Complexity:
The time complexities for the Max Heap CRUD (Create, Read, Update, Delete) operations are as follows:
-
Insertion (Create):
- Time Complexity: O(log n)
- Explanation: The worst-case time complexity for inserting an element into a max heap is logarithmic in the number of elements, as the element needs to be percolated up the height of the heap. The height of a binary heap is log(n) where n is the number of elements.
-
GetMax (Read):
- Time Complexity: O(1)
- Explanation: Retrieving the maximum element (root) in a max heap can be done in constant time as the maximum element is always at the root.
-
Update:
- Time Complexity: O(log n)
- Explanation: Updating an element in a max heap involves two operations: percolating up (up to log n steps) and max heapifying (up to log n steps). Therefore, the overall time complexity is logarithmic.
-
DeleteMax (Delete):
- Time Complexity: O(log n)
- Explanation: Deleting the maximum element involves replacing the root with the last element, which may require percolating down the height of the heap to maintain the heap property. The worst-case time complexity is logarithmic.
These time complexities assume that the underlying data structure is a binary heap. The actual performance may vary based on implementation details and the specific operations performed.
Space Complexity:
The space complexity for Max Heap CRUD (Create, Read, Update, Delete) operations is O(n), where n is the number of elements in the heap.
-
Insertion (Create):
- Explanation: The insertion operation generally doesn't require additional space proportional to the number of elements. The new element is added to the existing heap in-place.
-
GetMax (Read):
- Explanation: Reading the maximum element involves accessing the root of the heap. It doesn't require additional space proportional to the number of elements.
-
Update:
- Explanation: The update operation is performed in-place without requiring additional space.
-
DeleteMax (Delete):
- Explanation: The delete operation involves replacing the root with the last element and then adjusting the heap structure. It is performed in-place without requiring additional space.
Real-World Applications of MAX-HEAP CRUD(Create,Read,Update,Delete)
- Task Scheduling: Priority scheduling based on task priority levels.
- Job Scheduling: Allocating jobs to machines based on priority.
- Dijkstra's Algorithm: Finding the shortest path in a graph.
- Huffman Coding: Data compression algorithm.
- Order Processing: Managing orders based on their priority in e-commerce systems.
- Operating System Task Scheduling: Assigning priority to tasks for execution.
- Network Routing Algorithms: Determining the optimal path for data packets.
- Emergency Room Triage: Prioritizing patients based on the severity of their condition.
- Database Indexing: Managing indexes to speed up query performance.
- Wireless Sensor Networks: Energy-efficient data aggregation in sensor networks.
