MERGE SORT
MERGE SORT
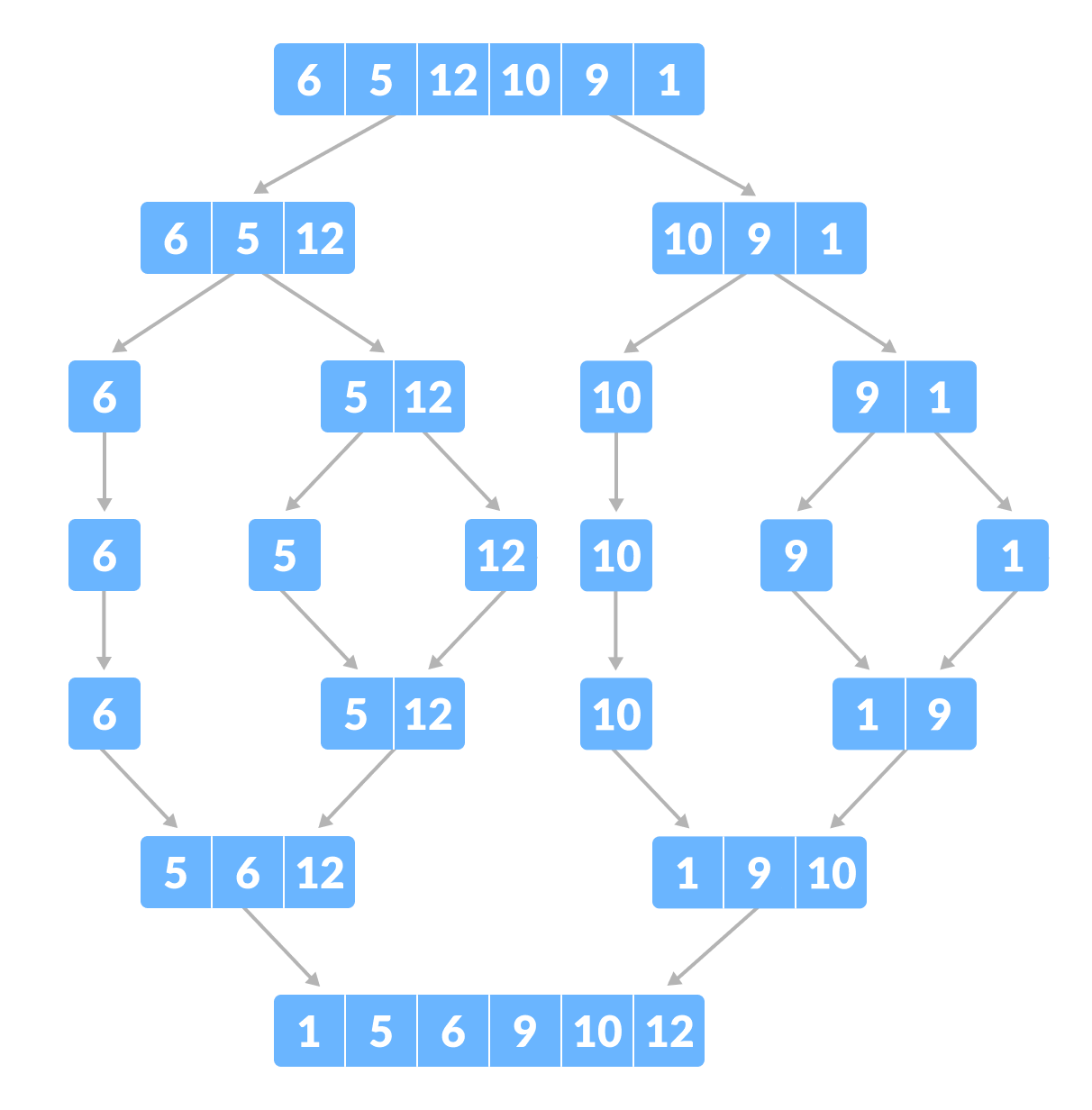
Merge sort is a popular sorting algorithm that follows the divide-and-conquer approach. It works by dividing the unsorted list into smaller sublists, sorting those sublists recursively, and then merging them back into a sorted list. This process continues until the entire list is sorted.
INTRODUCTION
The merge sort algorithm consists of two main steps: the divide step and the merge step. In the divide step, the unsorted list is divided into two halves until each sublist contains only one element or is empty. This is done recursively until all sublists are sorted.
In the merge step, the sorted sublists are merged back together by comparing the elements from each sublist and placing them in the correct order. This process continues until all sublists are merged into a single sorted list.
One of the key advantages of merge sort is its efficiency and stability. It has a time complexity of O(n log n) in the worst case, making it efficient for sorting large datasets. Additionally, merge sort is a stable sorting algorithm, meaning that it preserves the relative order of equal elements in the sorted list.
Overall, merge sort is a reliable and efficient sorting algorithm that is widely used in various applications. It provides a consistent performance and guarantees a sorted output, making it a valuable tool in computer science and data processing.
CODE
Python
#Copyrights to venkys.io
#For more programs visit venkys.io
#Python program for Merge sort
def merge_sort(array):
# Divide strategy
if len(array) > 1:
# Finding the mid index of the array
midx = len(array) // 2
# Dividing the array elements into left and right subarrays
Larray = array[:midx]
Rarray = array[midx:]
# Recursively apply merge_sort on left and right subarrays
merge_sort(Larray)
merge_sort(Rarray)
# Conquer strategy
idx1 = 0 # Initialize index for the left subarray
idx2 = 0 # Initialize index for the right subarray
idx = 0 # Initialize index for the merged array
# Merge the left and right subarrays in sorted order
while idx1 < len(Larray) and idx2 < len(Rarray):
if Larray[idx1] < Rarray[idx2]:
array[idx] = Larray[idx1]
idx1 += 1
else:
array[idx] = Rarray[idx2]
idx2 += 1
idx += 1
# Sorting the remaining elements in the left subarray
while idx1 < len(Larray):
array[idx] = Larray[idx1]
idx1 += 1
idx += 1
# Sorting the remaining elements in the right subarray
while idx2 < len(Rarray):
array[idx] = Rarray[idx2]
idx2 += 1
idx += 1
# Test drive code
if __name__ == "__main__":
# Reading the size of the array from STDIN
n = int(input("Enter the size of the array: "))
# Reading the array elements from STDIN
array = list(map(int, input("Enter the array elements separated by space: ").split()))
# Applying merge_sort to the array
merge_sort(array)
# Printing the sorted array
print("Sorted Array:", *array)
Step-by-Step Explanation:
- The merge_sort function takes an array as input and implements the merge sort algorithm.
- In the divide strategy, if the length of the array is greater than 1, the algorithm finds the mid index of the array and divides it into two halves.
- The left half of the array is assigned to the Larray variable, and the right half is assigned to the Rarray variable.
- The merge_sort function is called recursively for both the left and right halves to further divide them until each sublist contains only one element or is empty.
- In the conquer strategy, three index variables (idx1, idx2, and idx) are initialized to keep track of the position in the left array, right array, and original array, respectively.
- While both idx1 and idx2 are less than the lengths of Larray and Rarray respectively, the algorithm compares the elements at the corresponding positions and places the smaller element in the original array.
- After the previous step, there may be remaining elements in either Larray or Rarray. The algorithm then copies the remaining elements into the original array.
- Once the merge_sort function completes, the original array will be sorted in ascending order.
- The test drive code initializes an array with 7 elements and calls the merge_sort function on it.
- Finally, the sorted array is printed as output.
JAVA
// Copyrights to venkys.io
//For more programs visit venkys.io
//Java program for Merge sort
import java.util.Scanner;
public class MergeSort {
// Function to perform merge sort on the array
static void mergeSort(int[] array, int l, int r) {
if (l < r) {
int m = l + (r - l) / 2;
// Recursively calling mergeSort method to divide the array
mergeSort(array, l, m);
mergeSort(array, m + 1, r);
// Combines the divided array pieces in sorted order
merge(array, l, m, r);
}
}
// Function to merge two subarrays
static void merge(int[] array, int l, int m, int r) {
// Assigning sizes for temporary arrays
int n1 = m - l + 1;
int n2 = r - m;
// Temporary arrays to sort divided elements
int[] left = new int[n1];
int[] right = new int[n2];
// Assigning elements
for (int i = 0; i < n1; i++)
left[i] = array[l + i];
for (int j = 0; j < n2; j++)
right[j] = array[m + 1 + j];
// Initial indexes to sort elements using temporary arrays
int i = 0, j = 0;
// Index for the original array
int k = l;
// Comparing elements to arrange them in sorted order in the original array
while (i < n1 && j < n2) {
if (left[i] <= right[j]) {
array[k] = left[i];
i++;
} else {
array[k] = right[j];
j++;
}
k++;
}
// Arranging remaining elements from the left array
while (i < n1) {
array[k] = left[i];
i++;
k++;
}
// Arranging remaining elements from the right array
while (j < n2) {
array[k] = right[j];
j++;
k++;
}
}
// Function to print the sorted array
public static void printOutput(int[] array) {
System.out.println("The sorted order is:");
for (int a : array) {
System.out.print(a + " ");
}
System.out.println();
}
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter the size of the array: ");
int size = scanner.nextInt();
// Reading the array elements from STDIN
int[] array = new int[size];
System.out.print("Enter the array elements separated by space: ");
for (int i = 0; i < size; i++) {
array[i] = scanner.nextInt();
}
// Calling mergeSort for the entire array
mergeSort(array, 0, size - 1);
// Printing the sorted array
printOutput(array);
scanner.close();
}
}
Step-by-Step Explanation:
1.Import Statements: import java.util.Scanner;: Imports the Scanner class for reading input from the console.
2.Class Declaration: public class MergeSort {: Declares a class named MergeSort.
3.mergeSort Function: static void mergeSort(int[] array, int l, int r) {: This is the main function for the merge sort algorithm. if (l < r) {: Checks if the array has more than one element. int m = l + (r - l) / 2;: Calculates the middle index of the array. mergeSort(array, l, m);: Recursively calls mergeSort on the left subarray. mergeSort(array, m + 1, r);: Recursively calls mergeSort on the right subarray. merge(array, l, m, r);: Calls the merge function to combine the sorted subarrays.
4.merge Function: static void merge(int[] array, int l, int m, int r) {: Merges two sorted subarrays. int n1 = m - l + 1;: Calculates the size of the left subarray. int n2 = r - m;: Calculates the size of the right subarray. int[] left = new int[n1];: Creates a temporary array for the left subarray. int[] right = new int[n2];: Creates a temporary array for the right subarray. Copies elements from the original array to the temporary arrays. Initializes indexes (i, j, k) for merging the subarrays. Compares elements from the left and right subarrays and arranges them in sorted order.
5.printOutput Function: public static void printOutput(int[] array) {: Prints the sorted array. Iterates through the array and prints each element.
6.Main Function: public static void main(String args[]) {: The main function where the program execution begins. Creates a Scanner object to read input. Reads the size of the array (size) from the user. Creates an array (array) to store the elements. Reads the array elements from the user. Calls mergeSort to sort the array. Calls printOutput to print the sorted array. Closes the Scanner to release resources.
This program uses the merge sort algorithm to sort an array and prints the sorted order to the console. It takes user input for the size of the array and the array elements.
CPP
// Copyrights to venkys.io
// For more programs visit venkys.io
// CPP program for Merge sort
#include <iostream>
// Merge two subarrays of arr[]
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r) {
// Calculate sizes of the two subarrays
int n1 = m - l + 1;
int n2 = r - m;
// Create temporary arrays to store the data of the two subarrays
int left[n1];
int right[n2];
// Copy data to temporary arrays left[] and right[]
for (int i = 0; i < n1; i++) {
left[i] = arr[l + i];
}
for (int j = 0; j < n2; j++) {
right[j] = arr[m + 1 + j];
}
// Merge the temporary arrays back into arr[l..r]
int i = 0; // Initial index of the first subarray
int j = 0; // Initial index of the second subarray
int k = l; // Initial index of the merged subarray
// Compare elements of the two subarrays and merge them in ascending order
while (i < n1 && j < n2) {
if (left[i] <= right[j]) {
arr[k] = left[i];
i++;
} else {
arr[k] = right[j];
j++;
}
k++;
}
// Copy the remaining elements of left[], if there are any
while (i < n1) {
arr[k] = left[i];
i++;
k++;
}
// Copy the remaining elements of right[], if there are any
while (j < n2) {
arr[k] = right[j];
j++;
k++;
}
}
// Recursive function to perform merge sort on the array
void mergeSort(int arr[], int l, int r) {
if (l < r) {
// Same as (l+r)/2, but avoids overflow for large l and r
int m = l + (r - l) / 2;
// Recursively sort the first and second halves
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
// Merge the sorted halves
merge(arr, l, m, r);
}
}
int main() {
int n;
// Read the size of the array from STDIN
std::cout << "Enter the size of the array: ";
std::cin >> n;
int arr[n];
// Read the array elements from STDIN
std::cout << "Enter the array elements separated by space: ";
for (int i = 0; i < n; i++) {
std::cin >> arr[i];
}
// Call the merge sort function
mergeSort(arr, 0, n - 1);
// Print the sorted array
std::cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
std::cout << arr[i] << " ";
}
std::cout << std::endl;
return 0;
}
Step-by-Step Explanation:
1.Include Header: #include : Includes the iostream header for input and output operations.
2.Merge Function: void merge(int arr[], int l, int m, int r): Function to merge two sorted subarrays. Calculates sizes of two subarrays, creates temporary arrays, and copies data. Merges the temporary arrays back into the original array in sorted order.
3.Merge Sort Function: void mergeSort(int arr[], int l, int r): Recursive function for merge sort. Divides the array into two halves, recursively sorts each half, and then merges them.
4.Main Function: int main() {: The main function where the program execution begins. Reads the size of the array (n) from STDIN. Creates an array (arr) to store the elements. Reads the array elements from STDIN. Calls mergeSort to sort the array. Prints the sorted array to STDOUT.
5.Input and Output: std::cout << "Enter the size of the array: ";: Prompts the user to enter the size of the array. std::cin >> n;: Reads the size of the array from the user. std::cout << "Enter the array elements separated by space: ";: Prompts the user to enter the array elements. std::cin >> arr[i];: Reads each array element from the user. After sorting, the sorted array is printed to the console.
This program uses the merge sort algorithm to sort an array and interacts with the user through STDIN and STDOUT. The use of functions and comments enhances code readability and maintainability.
Time and Space complexity analysis:
The time and space complexity analysis for the merge sort algorithm is as follows:
Time Complexity:
- Best Case: O(n log n)
- Average Case: O(n log n)
- Worst Case: O(n log n)
The merge sort algorithm follows the divide-and-conquer approach, where the unsorted list is divided into smaller sublists until each sublist contains only one element or is empty. Then, the sorted sublists are merged back together to form a sorted list.
In each recursive call, the merge sort algorithm divides the list into two halves, which takes O(log n) time. Then, during the merge step, it compares and merges the elements from the sublists, which takes O(n) time in the worst case. Since the list is divided recursively into halves, the overall time complexity of merge sort is O(n log n).
Space Complexity: The space complexity of merge sort is O(n) because it requires auxiliary space to store the temporary subarrays during the merge step. In each recursive call, the merge sort algorithm creates temporary arrays to store the divided elements. The size of these temporary arrays is equal to the size of the original array, resulting in a space complexity of O(n).
Overall, merge sort is an efficient sorting algorithm with a time complexity of O(n log n) and a space complexity of O(n). It provides stable sorting, meaning that it preserves the relative order of equal elements in the sorted list. Merge sort is widely used in various applications where stability and efficiency are important factors.
Real-World Applications of Merge Sort:
Merge sort has several real-world applications due to its efficiency, stability, and ability to handle large datasets. Some notable applications of merge sort include:
- Sorting Algorithms: Merge sort is often used as a benchmark for other sorting algorithms due to its consistent performance and efficiency. It is commonly used to sort arrays, lists, and other data structures in programming languages.
- External Sorting: Merge sort's ability to efficiently handle large datasets makes it suitable for external sorting. External sorting is used when the data to be sorted exceeds the available memory. Merge sort's divide-and-conquer approach allows it to efficiently sort data that is too large to fit in memory by using disk-based operations.
- File Merge Operations: Merge sort is used in various file processing operations, such as merging multiple sorted files into a single sorted file. This is commonly seen in database systems, where large datasets are stored in multiple files and need to be merged for efficient querying and analysis.
- Inversion Count: Merge sort is also used to calculate the inversion count of an array. An inversion is a pair of elements in an array that are out of order. By counting the number of inversions, it is possible to measure the similarity between two datasets or to detect anomalies in data.
- External Merge Sort: Merge sort is a key component of external merge sort algorithms, which are used to sort large datasets that do not fit entirely in memory. External merge sort divides the data into smaller chunks, sorts them using merge sort, and then merges the sorted chunks to produce the final sorted result.
- Parallel Computing: Merge sort can be parallelized, making it suitable for parallel computing environments. By dividing the data and sorting the sublists in parallel, merge sort can achieve faster sorting times on systems with multiple processors or cores.
Overall, merge sort's efficiency, stability, and ability to handle large datasets make it a valuable tool in various real-world applications that involve sorting and managing large amounts of data.
