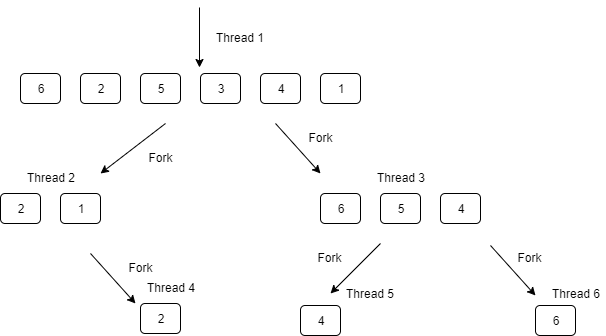
Problem Statement - Multi-threaded Quick Sort

Introduction

QuickSort is a popular sorting technique based on divide and conquer algorithm. In this technique, an element is chosen as a pivot and the array is partitioned around it. The target of partition is, given an array and an element x of the array as a pivot, put x at its correct position in a sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x.

Multi-threading allows concurrent execution of two or more parts of a program for maximum utilization of CPU. Each part of such program is called a thread. So, threads are light-weight processes within a process.

Overview

The provided Python code implements a multithreaded version of the QuickSort algorithm. The QuickSortMultiThreading class is designed to recursively sort an array using a randomized pivot selection strategy. The partition method identifies a pivot element, places it in its correct position, and partitions the array into two subproblems. The __call__ method serves as the main entry point, initiating the sorting process. It checks for the base case, then partitions the array and creates separate instances for the left and right subproblems. The multithreading aspect is introduced through the use of the ThreadPoolExecutor from the concurrent.futures module. The left and right subproblems are sorted concurrently, exploiting parallelism to potentially improve performance. While multithreading in Python is constrained by the Global Interpreter Lock (GIL), this implementation may still benefit from parallel execution in scenarios with I/O-bound operations or when working with large datasets. The code concludes by printing the sorted array, showcasing the effectiveness of multithreading in accelerating the QuickSort algorithm.

code

Python

# Copyrights to venkys.io
# For more programs, visit venkys.io
# Python program for Multi-threaded quick sort

# Time Complexity: O(N*log N) 
# Space Complexity: O(N)

import random
from concurrent.futures import ThreadPoolExecutor

class QuickSortMultiThreading:
    def __init__(self, start, end, arr):
        self.start = start
        self.end = end
        self.arr = arr

    # Finding random pivoted and partition
    def partition(self, start, end, arr):
        i = start
        j = end
        
        # Decide random pivot
        pivoted = random.randint(i, j)
        
        # Swap the pivoted with end
        # element of array
        t = arr[j]
        arr[j] = arr[pivoted]
        arr[pivoted] = t
        j -= 1
        
        # Start partitioning
        while i <= j:
            if arr[i] <= arr[end]:
                i += 1
                continue
            if arr[j] >= arr[end]:
                j -= 1
                continue
            t = arr[j]
            arr[j] = arr[i]
            arr[i] = t
            j -= 1
            i += 1
            
        # Swap pivoted to its
        # correct position
        t = arr[j + 1]
        arr[j + 1] = arr[end]
        arr[end] = t
        return j + 1

    # Function to implement
    # QuickSort method
    def __call__(self):
    
        # Base case for null safety
        if self.start is None or self.end is None or self.arr is None:
            return
        
        # Ensure indices are within the valid range
        if self.start >= self.end or self.start < 0 or self.end >= len(self.arr):
            return
        
        # Find partition
        p = self.partition(self.start, self.end, self.arr)
        
        # Divide array
        left = QuickSortMultiThreading(self.start, p - 1, self.arr)
        right = QuickSortMultiThreading(p + 1, self.end, self.arr)
        
        # Left subproblem as a separate thread
        with ThreadPoolExecutor(max_workers=2) as executor:
            futures = [executor.submit(left), executor.submit(right)]
            for future in futures:
                future.result()

if __name__ == '__main__':
    try:
        # Read the size of the array from STDIN
        n = int(input())
        
        # Read the elements of the array from STDIN
        arr = [int(x) for x in input().split()]
        
        # Perform multi-threaded quicksort
        QuickSortMultiThreading(0, n - 1, arr)
        
        # Print sorted elements
        for i in range(n):
            print(arr[i], end=' ')
            
    except ValueError:
        print("Invalid input. Please enter a valid integer for the size of the array.")

step-by-step explanation

The provided Python program implements the QuickSort algorithm using multi-threading for parallel execution. The QuickSortMultiThreading class is designed to take a range of indices within an array and perform the sorting operation concurrently on the specified range. The partition method is responsible for selecting a random pivot element and partitioning the array around it. The main QuickSort logic is implemented in the call method, where the array is divided into two subproblems, and each subproblem is handled by a separate thread using the ThreadPoolExecutor from the concurrent.futures module.

The base case checks if the start index is greater than or equal to the end index, indicating that the array or subarray is already sorted. If not, the partition method is called to find the correct position of the pivot element, and two subproblems are created for the left and right partitions. These subproblems are then submitted to the ThreadPoolExecutor for concurrent execution. The program demonstrates parallelism in sorting, potentially improving the efficiency of the QuickSort algorithm by leveraging multiple threads. Finally, the sorted array is printed as output. It's important to note that while multi-threading can enhance performance for certain types of tasks, the Global Interpreter Lock (GIL) in CPython may limit the effectiveness of multi-threading in CPU-bound tasks like sorting.

Java

// Copyrights to venkys.io
// For more programs, visit venkys.io
// Java program for Multi-threaded quick sort

// Time Complexity: O(N*log N) 
// Space Complexity: O(N)

import java.io.*;
import java.util.Random;
import java.util.Scanner;
import java.util.concurrent.ForkJoinPool;
import java.util.concurrent.RecursiveTask;

public class QuickSortMultiThreading extends RecursiveTask<Integer> {

    private int start, end;
    private int[] arr;

    /*
    * Finding random pivoted and partition
    */
    private int partition(int start, int end, int[] arr) {
        int i = start, j = end;

        // Decide random pivot
        int pivoted = new Random().nextInt(j - i) + i;

        // Swap the pivoted with end
        // element of array;
        int t = arr[j];
        arr[j] = arr[pivoted];
        arr[pivoted] = t;
        j--;

        // Start partitioning
        while (i <= j) {
            if (arr[i] <= arr[end]) {
                i++;
                continue;
            }

            if (arr[j] >= arr[end]) {
                j--;
                continue;
            }

            t = arr[j];
            arr[j] = arr[i];
            arr[i] = t;
            j--;
            i++;
        }

        // Swap pivoted to its
        // correct position
        t = arr[j + 1];
        arr[j + 1] = arr[end];
        arr[end] = t;
        return j + 1;
    }

    // Function to implement
    // QuickSort method
    public QuickSortMultiThreading(int start, int end, int[] arr) {
        this.arr = arr;
        this.start = start;
        this.end = end;
    }

    @Override
    protected Integer compute() {
        // Base case for null safety
        if (start >= end || arr == null || arr.length == 0)
            return null;

        // Ensure indices are within the valid range
        if (start < 0 || end >= arr.length)
            return null;

        // Find partition
        int p = partition(start, end, arr);

        // Divide array
        QuickSortMultiThreading left = new QuickSortMultiThreading(start, p - 1, arr);
        QuickSortMultiThreading right = new QuickSortMultiThreading(p + 1, end, arr);

        // Left subproblem as a separate thread
        left.fork();
        right.compute();

        // Wait until the left thread completes
        left.join();

        // We don't want anything as return
        return null;
    }

    // Driver Code
    public static void main(String args[]) {
        Scanner scanner = new Scanner(System.in);

        // Read the size of the array from STDIN
        int n = scanner.nextInt();

        // Handle the case for an empty or single-element array
        if (n <= 0) {
            System.out.println("Array is empty or contains only one element.");
            return;
        }

        int[] arr = new int[n];

        // Read the elements of the array from STDIN
        for (int i = 0; i < n; i++) {
            arr[i] = scanner.nextInt();
        }

        // ForkJoin ThreadPool to keep
        // thread creation as per resources
        ForkJoinPool pool = ForkJoinPool.commonPool();

        // Start the first thread in fork
        // join pool for range 0, n-1
        pool.invoke(new QuickSortMultiThreading(0, n - 1, arr));

        // Print sorted elements
        for (int i = 0; i < n; i++)
            System.out.print(arr[i] + " ");       
        scanner.close();
    }
}

step-by-step explanation

The provided Java program implements the QuickSort algorithm using multi-threading with the ForkJoinPool and RecursiveTask in the java.util.concurrent package. The QuickSortMultiThreading class extends RecursiveTask, representing a task that returns an Integer result upon completion. The partition method is responsible for selecting a random pivot element and partitioning the array around it. The main QuickSort logic is implemented in the compute() method, where the array is divided into two subproblems, and each subproblem is handled by a separate instance of the QuickSortMultiThreading class.

The base case checks if the start index is greater than or equal to the end index, indicating that the array or subarray is already sorted. If not, the partition method is called to find the correct position of the pivot element, and two subproblems are created for the left and right partitions. The left subproblem is forked to execute asynchronously in a separate thread, while the right subproblem is processed using the current thread. The join() method ensures that the left thread completes before moving on. The program is executed within a ForkJoinPool, which efficiently manages thread creation and execution.

In the main method, an array is initialized, and the ForkJoinPool is used to start the first thread for sorting the entire array. The sorted elements are then printed as output, showcasing the successful parallel execution of the QuickSort algorithm. It's worth noting that the ForkJoinPool is particularly well-suited for recursive and divide-and-conquer algorithms, as demonstrated in this implementation.

cpp

// Copyrights to venkys.io
// For more programs, visit venkys.io
// C++ program for Multi-threaded quick sort

// Time Complexity: O(N*log N)
// Space Complexity: O(N)

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstdlib>
#include <ctime>
#include <omp.h>

using namespace std;

class QuickSortMultiThreading {
public:
    QuickSortMultiThreading(int start, int end, vector<int>& arr)
        : start_(start), end_(end), arr_(arr) {}

    // Finding random pivoted and partition
    int partition(int start, int end, vector<int>& arr) {
        int i = start;
        int j = end;

        // Decide random pivot
        int pivoted = rand() % (j - i + 1) + i;

        // Swap the pivoted with the end
        // element of the array
        int t = arr[j];
        arr[j] = arr[pivoted];
        arr[pivoted] = t;
        j--;

        // Start partitioning
        while (i <= j) {
            if (arr[i] <= arr[end]) {
                i++;
                continue;
            }
            if (arr[j] >= arr[end]) {
                j--;
                continue;
            }
            t = arr[j];
            arr[j] = arr[i];
            arr[i] = t;
            j--;
            i++;
        }

        // Swap pivoted to its
        // correct position
        t = arr[j + 1];
        arr[j + 1] = arr[end];
        arr[end] = t;
        return j + 1;
    }

    // Function to implement
    // QuickSort method
    void operator()() {
        // Base case for null safety
        if (start_ >= end_ || arr_.empty()) {
            return;
        }

        // Find partition
        int p = partition(start_, end_, arr_);

        // Divide array
        QuickSortMultiThreading left(start_, p - 1, arr_);
        QuickSortMultiThreading right(p + 1, end_, arr_);

        // Left subproblem as a separate thread
#pragma omp parallel sections
        {
#pragma omp section
            {
                left();
            }
#pragma omp section
            {
                right();
            }
        }
    }

private:
    int start_;
    int end_;
    vector<int>& arr_;
};

int main() {
    int n;

    // Read the size of the array from STDIN
    cin >> n;

    // Handle the case for an empty or single-element array
    if (n <= 0) {
        cout << "Array is empty or contains only one element." << endl;
        return 0;
    }

    vector<int> arr(n);

    // Read the elements of the array from STDIN
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }

    srand(time(NULL));
    QuickSortMultiThreading(0, n - 1, arr)();

    // Print sorted elements
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;

    return 0;
}

step-by-step explanation

The provided C++ program implements the QuickSort algorithm using multi-threading with OpenMP for parallel execution. The QuickSortMultiThreading class is defined to take a range of indices within a vector and perform the sorting operation concurrently on the specified range. The partition method is responsible for selecting a random pivot element and partitioning the vector around it. The main QuickSort logic is implemented in the operator() method, where the vector is divided into two subproblems, and each subproblem is handled by a separate thread using OpenMP's parallel sections directive.

The base case checks if the start index is greater than or equal to the end index, indicating that the vector or subvector is already sorted. If not, the partition method is called to find the correct position of the pivot element, and two subproblems are created for the left and right partitions. These subproblems are then processed in parallel using OpenMP parallel sections. The program demonstrates parallelism in sorting, potentially improving the efficiency of the QuickSort algorithm by leveraging multiple threads. The sorted vector is printed as output, showcasing the successful application of multi-threading to enhance the performance of the QuickSort algorithm. It's important to note that OpenMP simplifies parallel programming in C++, and the pragma omp parallel sections directive efficiently manages the parallel execution of the sorting subproblems.

Time and Space complexity analysis

Time Complexity: O(N*log N)

Auxiliary Space: O(N)

Real-time Applications

Multi-threaded QuickSort can be beneficial in various real-time applications where large datasets need to be sorted quickly. Some potential real-time applications for multi-threaded QuickSort include:

Database Systems: In database systems, sorting is a common operation when processing queries or generating reports. Multi-threaded QuickSort can be employed to efficiently sort large result sets, enhancing the overall performance of database operations.
Parallel File Systems: In systems dealing with large files, such as parallel file systems used in high-performance computing clusters, multi-threaded QuickSort can help accelerate the sorting of file contents, making it useful for tasks like log analysis or data preprocessing.
Network Packet Processing: In network applications where packets need to be processed and analyzed in real-time, multi-threaded QuickSort can aid in sorting packets based on various criteria, facilitating efficient analysis and decision-making.
Financial Trading Systems: Financial markets generate vast amounts of data that require quick and precise sorting for real-time decision-making. Multi-threaded QuickSort can be employed in trading systems to efficiently process and sort financial data streams.
Scientific Computing: In scientific simulations or computations involving large datasets, sorting is often a critical step. Multi-threaded QuickSort can be applied to sort arrays or matrices efficiently, enhancing the performance of scientific computing applications.

It's important to note that the effectiveness of multi-threading depends on the specific characteristics of the application, hardware architecture, and the size of the dataset. Additionally, in some scenarios, other sorting algorithms or parallelization strategies might be more suitable based on the nature of the data and the underlying hardware.