POST ORDER TRAVERSALS
POST ORDER TRAVERSALS
Tree Traversals:
Traversing a tree means visiting every node in the tree. You might, for instance, want to add all the values in the tree or find the largest one. For all these operations, you will need to visit each node of the tree.
Linear data structures like arrays, stacks ,queues and linked list have only one way to read the data. But a hierarchical data structure like a tree can be traversed in different ways.
In order Traversal:
- Traverse the left subtree in in order.
- Visit the current node.
- Traverse the right subtree in in order.
The result is that nodes are visited in ascending order in a binary search tree (BST).
-
Preorder Traversal:
- Visit the current node.
- Traverse the left subtree in preorder.
- Traverse the right subtree in preorder.
This traversal is often used in creating a prefix notation of mathematical expressions.
-
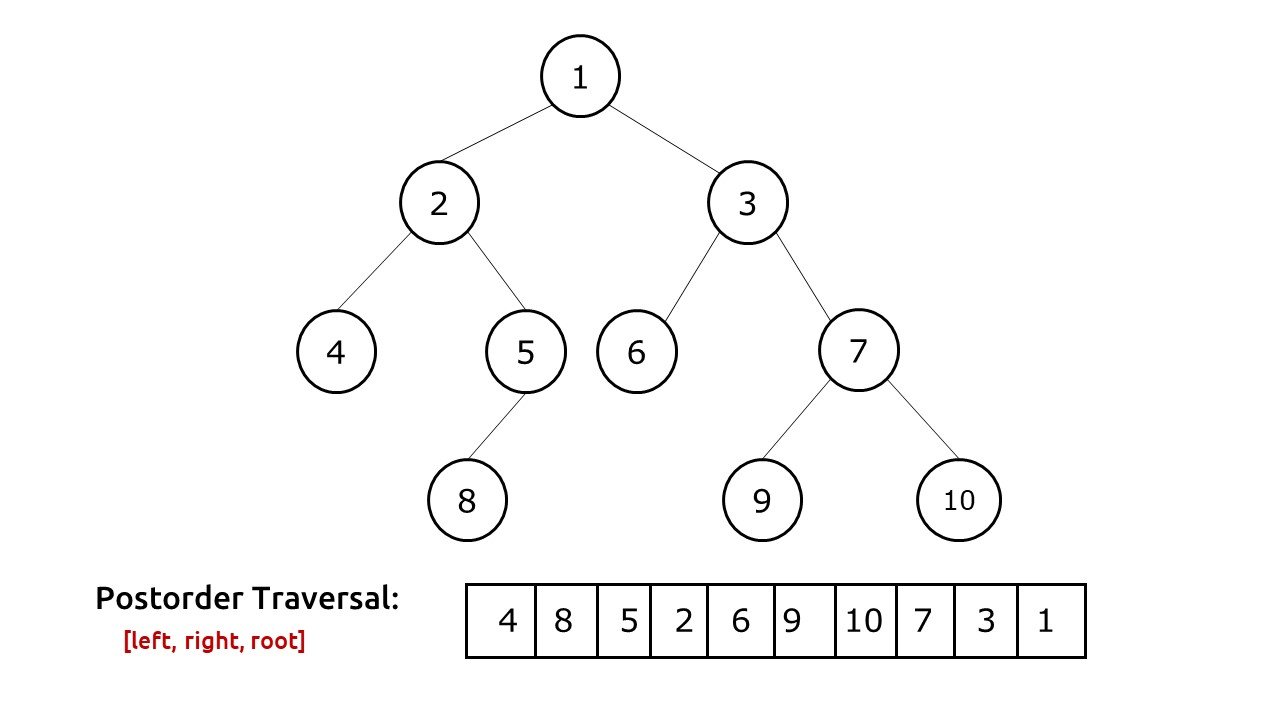
Post order Traversal:
- Traverse the left subtree in post order.
- Traverse the right subtree in post order.
- Visit the current node.
This traversal is commonly used in expression tree evaluations and certain types of mathematical calculations.
Introduction to post order traversal:
The post order traversal technique follows the Left Right Root policy. Here, Left Right Root means the left subtree of the root node is traversed first, then the right subtree, and finally, the root node is traversed. Here, the Post order name itself suggests that the tree's root node would be traversed at last.
Post order traversal is a binary tree traversal method where nodes are visited in the order of left subtree, right subtree, and then the root. This sequence is crucial in expression tree evaluations, yielding postfix expressions. It's employed in mathematical computations, especially when processing operands before operators. The order also facilitates memory management and parsing algorithms, ensuring child nodes are processed prior to their parents. In practical terms, post order traversal is a valuable technique for various applications, offering a specific order of node visitation that is exploited in algorithm design, data structure manipulation, and mathematical calculations involving binary trees.
Overview of post order traversal
- Traverse the left subtree in post order: Recursively apply the post order traversal algorithm to the left subtree of the current node.
- Traverse the right subtree in post order: Recursively apply the post order traversal algorithm to the right subtree of the current node.
- Visit the root node: Process or print the value of the current node.
So, the correct overview for post order traversal is:
- Traverse the left subtree.
- Traverse the right subtree.
- Visit the root node.
The order is left subtree, right subtree, and then the root. This ensures that you first explore the entire left subtree, then the entire right subtree, and finally, you visit the current node.
code:
class Node:
def __init__(self,data):
self.data=data
self.left=self.right=None
def VSDpostorder(root):
if root:
VSDpostorder(root.left)
VSDpostorder(root.right)
print(root.data)
if __name__=="__main__":
root_data = int(input())
root = Node(root_data)
left_data = int(input())
if left_data != -1:
root.left = Node(left_data)
right_data = int(input())
if right_data != -1:
root.right = Node(right_data)
left_left_data = int(input())
if left_left_data != -1:
root.left.left = Node(left_left_data)
left_right_data = int(input())
if left_right_data != -1:
root.left.right = Node(left_right_data)
right_left_data = int(input())
if right_left_data != -1:
root.right.left = Node(right_left_data)
right_right_data = int(input())
if right_right_data != -1:
root.right.right = Node(right_right_data)
VSDpostorder(root)
#include <iostream>
#include <queue>
class Node {
public:
int data;
Node* left;
Node* right;
Node(int val) : data(val), left(nullptr), right(nullptr) {}
};
void postorder(Node* root) {
if (root != nullptr) {
postorder(root->left);
postorder(root->right);
std::cout << root->data << " ";
}
}
Node* buildBinaryTree() {
int root_data;
// std::cout << "Enter value for root node: ";
std::cin >> root_data;
Node* root = new Node(root_data);
std::queue<Node*> nodes_queue;
nodes_queue.push(root);
while (!nodes_queue.empty()) {
Node* current = nodes_queue.front();
nodes_queue.pop();
int left_data, right_data;
// std::cout << "Enter value for left child of " << current->data << " (or -1 if none): ";
std::cin >> left_data;
if (left_data != -1) {
current->left = new Node(left_data);
nodes_queue.push(current->left);
}
// std::cout << "Enter value for right child of " << current->data << " (or -1 if none): ";
std::cin >> right_data;
if (right_data != -1) {
current->right = new Node(right_data);
nodes_queue.push(current->right);
}
}
return root;
}
int main() {
Node* root = buildBinaryTree();
// std::cout << "Post-order traversal of the binary tree:" << std::endl;
postorder(root);
// Free memory
// Implement deletion of tree nodes if necessary
return 0;
}
import java.util.Scanner;
class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
this.left = null;
this.right = null;
}
}
public class Main {
static Scanner scanner = new Scanner(System.in);
static void postorder(Node root) {
if (root != null) {
postorder(root.left);
postorder(root.right);
System.out.print(root.data + " ");
}
}
static Node buildBinaryTree() {
// System.out.print("Enter value for root node: ");
int rootData = scanner.nextInt();
Node root = new Node(rootData);
buildChildNodes(root, "root");
return root;
}
static void buildChildNodes(Node parent, String position) {
// System.out.print("Enter value for " + position + " left child (or -1 if none): ");
int leftData = scanner.nextInt();
if (leftData != -1) {
parent.left = new Node(leftData);
buildChildNodes(parent.left, "left child of " + parent.data);
}
// System.out.print("Enter value for " + position + " right child (or -1 if none): ");
int rightData = scanner.nextInt();
if (rightData != -1) {
parent.right = new Node(rightData);
buildChildNodes(parent.right, "right child of " + parent.data);
}
}
public static void main(String[] args) {
Node root = buildBinaryTree();
// System.out.println("Post-order traversal of the binary tree:");
postorder(root);
}
}
step by step explanation:
Let’s now examine the post order traversal algorithm.
For all nodes of the tree:
Step 1: Firstly, we traverse the left sub element repeatedly.
Step 2: Now, in the second stage, we traverse the right sub element repeatedly.
Step 3: Visit the root node.
Time Complexity:
The time complexity of the post order traversal of a binary tree is O(n), where "n" is the number of nodes in the tree. This is because, in the worst case, you need to visit and process each node once.
Let's break it down:
- At each node, you perform a constant amount of work (processing the node).
- Since you visit each node once, the total time complexity is proportional to the number of nodes in the tree.
Therefore, the time complexity for post order traversal, as well as for other depth-first traversal methods (preorder and in order), is O(n), where "n" is the number of nodes in the binary tree.
Space Complexity
In this iterative approach, the space complexity is also influenced by the size of the stack. It's O(h) or O(n), where h is the height of the binary tree and n is the number of nodes.
The iterative approach might require additional space for the result list, but this is often not considered in the space complexity analysis as it depends on the specific requirements of the problem. If we only consider the space required for traversal logic, it remains O(h) or O(n).
Real World Applications:
Post order traversal of binary trees has several real-world applications in various fields. Here are some examples:
- Dependency Resolution:
- Post order traversal can be used in dependency resolution scenarios. For example, in a project with dependencies, post order traversal ensures that dependent components are built or processed before their dependents.
- Mathematical Calculations:
- Post order traversal is used in mathematical calculations involving binary trees. For example, when evaluating mathematical expressions stored in a binary tree, post order traversal ensures that operands are processed before their corresponding operators.
- Memory Management:
- In certain memory management scenarios, post order traversal can be applied for efficient deallocation of resources associated with tree nodes. This order ensures that child nodes are processed before their parents, which is helpful in dynamic memory management.
- Syntax Tree Processing:
- In parsing algorithms for compilers and interpreters, post order traversal is used to process the nodes of a syntax tree. It helps in ensuring the correct order of operations and evaluations.
- File System Operations:
- Post order traversal can be applied in file systems to perform operations such as deleting a directory and its contents. This ensures that the contents of a directory are deleted before the directory itself.
- Decision Tree Processing:
- In machine learning, particularly with decision trees, post order traversal can be employed to interpret and analyze the structure of the tree. This is useful for understanding the decision-making process.
Test Cases:
-
Input: let's input values to construct a binary tree: 10 20 30 -1 -1 -1 -1 -1 Output: The output will be the post-order traversal of the constructed binary tree.
For the provided input, the output would be: 20 30 10
Explanation: The input constructs a binary tree where the root node has a value of 10, and it has no children. The post-order traversal starts from the root: Since the left and right children of the root are None, it directly prints the value of the root node, which is 10. Therefore, the post-order traversal output is 20 30 10, which represents the data of the nodes visited in post-order traversal.
-
Input: let's input values to construct a binary tree: 1 2 3 4 5 -1 -1 6 7 -1 -1 -1
Output: The output will be the post-order traversal of the constructed binary tree. For the provided input, the output would be: 4 5 2 6 7 3 1
Explanation: The input constructs a binary tree where the root node has a value of 1. The left child of the root has a value of 2, and the right child has a value of 3. The left child of node 2 has a value of 4, and the right child has a value of 5. The left child of node 3 has no child (-1), and the right child has a value of 6. The right child of node 6 has a value of 7. The post-order traversal visits the nodes in the following order: Traverse left subtree of root 1: 4, 5, 2 Traverse right subtree of root 1: 6, 7, 3 Finally, print root node 1 Therefore, the post-order traversal output is 4 5 2 6 7 3 1, which represents the data of the nodes visited in post-order traversal.
