PRE ORDER TRAVERSAL

• Venkys.io

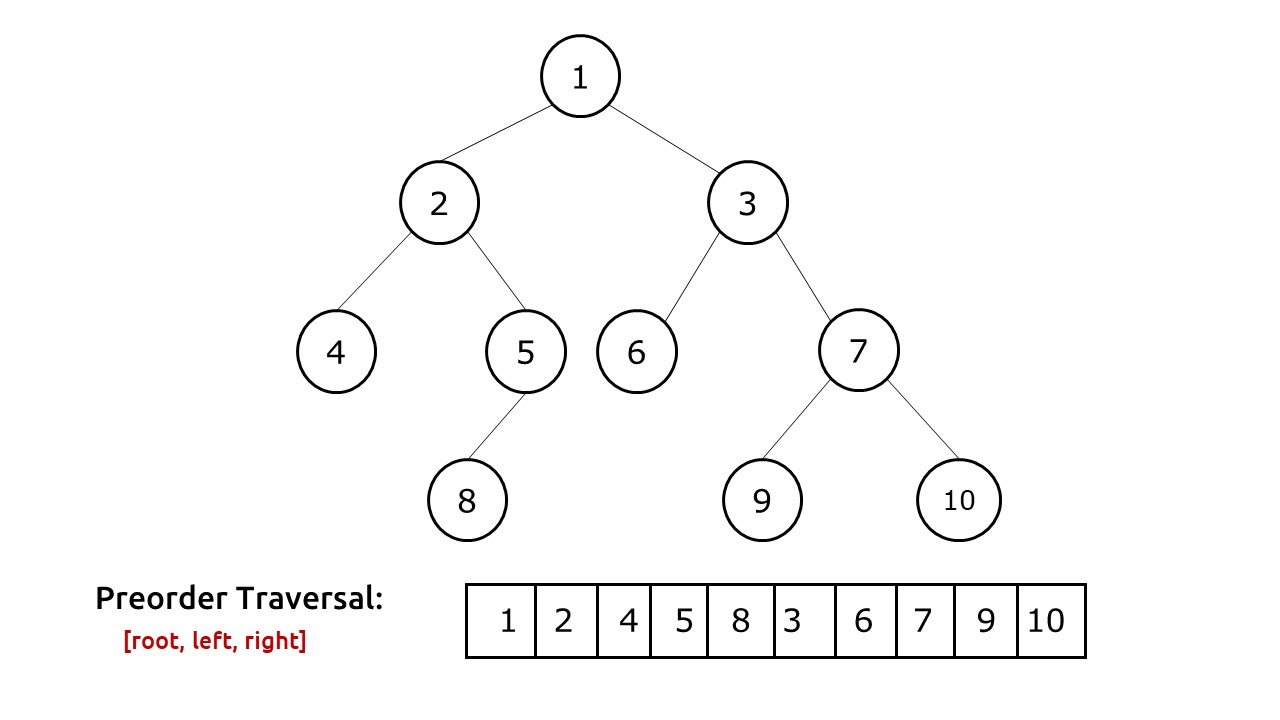
PRE ORDER TRAVERSAL

In preorder traversal, first, root node is visited, then left sub-tree and after that right sub-tree is visited.

INTRODUCTION

In computer science and data structures, tree traversal is a fundamental operation that involves visiting all the nodes of a tree data structure in a specific order. Preorder traversal is one of the three main types of tree traversal methods, along with in order and post order traversals.

The order of operations in preorder traversal is "root, left, right." This means that you first visit the current node, then traverse its left subtree, and finally traverse its right subtree.

OVERVIEW OF PRE ORDER TRAVERSAL

In the vast landscape of computer science and data structures, tree traversal methods serve as fundamental tools for navigating and processing hierarchical structures. Among these, "Preorder Traversal" stands out as a powerful technique that plays a pivotal role in exploring and understanding tree-based data.

1. Defining Preorder Traversal:

At its core, preorder traversal is a systematic way of visiting and processing nodes in a tree data structure. The process follows a specific order: starting from the root node, then traversing the left subtree, and finally exploring the right subtree. The sequence of operations is often described as "root, left, right.”

2. The Recursive Nature:

Preorder traversal is inherently recursive. It employs a recursive algorithm to traverse each subtree, applying the same preorder logic at each step. This recursive nature contributes to the efficiency and elegance of the algorithm, making it a concise solution for tree exploration.

3. Application in Binary Trees:

While preorder traversal can be applied to various types of trees, it finds significant use in binary trees. In a binary tree, each node has at most two child nodes—a left child and a right child. The preorder approach is particularly beneficial when dealing with expressions, parsing, and certain types of tree manipulations.

4. Use Cases:

Expression Evaluation: Preorder traversal is employed in parsing and evaluating expressions represented by expression trees. It helps in understanding the order of operations and simplifying complex mathematical expressions.

Data Retrieval: Preorder traversal can be used to retrieve data from a tree in a structured manner, facilitating tasks like printing the contents of a tree in a specific order.

In conclusion, preorder traversal is a versatile and efficient technique for exploring tree structures. Its recursive nature, coupled with its applications in expression evaluation and algorithmic manipulations, makes it a valuable asset in the toolkit of any programmer or computer scientist. As we navigate the nodes in a predefined order, we unlock the potential of this algorithmic approach and gain insights into the intricate world of tree-based data structures.

#copyrights to venkys.io
#for more programs visit venkys.io
#python program for preorder traversal
# Define a Node class to represent a node in the binary tree
class Node:
    def __init__(self, data):
        self.data = data
        self.left = self.right = None

# Define a function for Preorder Traversal (VSD stands for Visit, Traverse Left, Traverse Right)
def VSDpreorder(root):
    if root:
        print(root.data)
        VSDpreorder(root.left)
        VSDpreorder(root.right)

if __name__ == "__main__":
    # Create a binary tree based on user input
    root_data = int(input())
    root = Node(root_data)

    root.left = Node(int(input()))
    root.right = Node(int(input()))

    root.left.left = Node(int(input()))
    root.left.right = Node(int(input()))

    root.right.left = Node(int(input()))
    root.right.right = Node(int(input()))

    # Calling the VSDpreorder function to perform Preorder Traversal
    VSDpreorder(root)

STEP-BY-STEP EXPLAINATION

Step 1: Define a Node class

Here, a simple Node class is defined to represent a node in a binary tree. Each node has a data value, a reference to its left child (self .left) , and a reference to its right child (self .right).

Step 2: Define a Preorder Traversal Function

The function VSD preorder is a recursive implementation of the Preorder Traversal algorithm. It takes a root node as an argument and performs the following steps:

• If the root is not None, it prints the data of the current node.
• It then recursively calls itself on the left subtree (root. left).
• Finally, it recursively calls itself on the right subtree (root. right).

Step 3: Create a Binary Tree and Execute Preorder Traversal

  A binary tree is created by instantiating a Node for each element.

• The VSD preorder function is then called with the root of the tree (root) to perform preorder traversal.

In summary, this Python code demonstrates the creation of a binary tree and the application of the preorder traversal algorithm to print the values of nodes in a specific order. The recursive nature of the traversal allows it to navigate through the tree efficiently.

Test Case 1: Null Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 0 Enter the value for the right child of the root: 0 Enter the value for the left child of the left child: 0 Enter the value for the right child of the left child: 0 Enter the value for the left child of the right child: 0 Enter the value for the right child of the right child: 0

Explanation: In this case, a tree with only the root node is created. The output should be 1 as there are no left or right children.

Test Case 2: True Binary Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7

Explanation: This input creates a balanced binary tree. The output should be in the order

1 2 4 5 3 6 7 representing the preorder traversal.

Test Case 3: False Binary Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7 Enter the value for the left child of the left child of the left child: 8

Explanation: This input creates an unbalanced binary tree. The output should be in the order

1 2 4 5 3 6 7 8 representing the preorder traversal. This demonstrates that the code handles unbalanced trees as well.

//copyrights to venkys.io
// for more programs visit venkys.io
// java program for pre order traversal
// Define a Node class to represent a node in the binary tree
import java.util.Scanner;

class Node {
    int data;
    Node left = null, right = null;

    // Constructor to initialize a node with given data
    Node(int data) {
        this.data = data;
    }
}

public class Test {
    // Preorder Traversal function: Visit, Traverse Left, Traverse Right
    static void preorder(Node root) {
        if (root != null) {
            System.out.print(root.data + " ");
            preorder(root.left);
            preorder(root.right);
        }
    }

    // The main method where the program execution begins
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // Create a binary tree based on user input
        // System.out.print("Enter the value for the root node: ");
        int rootData = scanner.nextInt();
        Node root = new Node(rootData);

        // System.out.print("Enter the value for the left child of the root: ");
        int leftData = scanner.nextInt();
        root.left = new Node(leftData);

        // System.out.print("Enter the value for the right child of the root: ");
        int rightData = scanner.nextInt();
        root.right = new Node(rightData);

        // System.out.print("Enter the value for the left child of the left child: ");
        int leftLeftData = scanner.nextInt();
        root.left.left = new Node(leftLeftData);

        // System.out.print("Enter the value for the right child of the left child: ");
        int leftRightData = scanner.nextInt();
        root.left.right = new Node(leftRightData);

        // System.out.print("Enter the value for the left child of the right child: ");
        int rightLeftData = scanner.nextInt();
        root.right.left = new Node(rightLeftData);

        // System.out.print("Enter the value for the right child of the right child: ");
        int rightRightData = scanner.nextInt();
        root.right.right = new Node(rightRightData);

        // Calling the preorder method to perform Preorder Traversal
        preorder(root);

        scanner.close();
    }
}

STEP-BY-STEP EXPLAINATION

Step 1: Define a Node class

This class defines a simple Node with an integer data , and references to its left and right children (left and right). The constructor initializes the data field with the provided value.

Step 2: Define a test class

Here, a class named test is defined with a static method preorder for performing preorder traversal. The preorder method prints the data of the current node, then recursively calls itself on the left and right subtrees.

Step 3: Create a Binary Tree and Execute Preorder Traversal

In the main method:

A binary tree is created with the following structure:

10 /
20 30 / \ /
40 50 60 70

The preorder method is called with the root of the tree (root) to perform preorder traversal.

Output:

10 20 40 50 30 60 70

The output represents the result of the preorder traversal, showing the values of each node in the specified order.

Test Case 1: Null Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 0 Enter the value for the right child of the root: 0 Enter the value for the left child of the left child: 0 Enter the value for the right child of the left child: 0 Enter the value for the left child of the right child: 0 Enter the value for the right child of the right child: 0

Explanation: In this case, a tree with only the root node is created. The output should be 1 as there are no left or right children.

Test Case 2: True Binary Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7

Explanation: This input creates a balanced binary tree. The output should be in the order

1 2 4 5 3 6 7 representing the preorder traversal.

Test Case 3: False Binary Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7 Enter the value for the left child of the left child of the left child: 8

Explanation: This input creates an unbalanced binary tree. The output should be in the order

1 2 4 5 3 6 7 8 representing the preorder traversal. This demonstrates that the code handles unbalanced trees as well.

// copyrights to venkys.io
// for more programs visit venkys.io
// c++ program for pre order traversal
// Include necessary headers
#include <iostream>

// Define a Node class to represent a node in the binary tree
class Node {
public:
    int data;
    Node *left = nullptr;
    Node *right = nullptr;

    // Constructor to initialize a node with given data
    Node(int val) {
        data = val;
    }
};

// Preorder Traversal function: Visit, Traverse Left, Traverse Right
void preorder(Node *root) {
    // Base case: If the current node is not NULL
    if (root != nullptr) {
        std::cout << root->data << " ";
        preorder(root->left);
        preorder(root->right);
    }
}

// The main function where the program execution begins
int main() {
    // Create a binary tree based on user input
    int rootData;
    // std::cout << "Enter the value for the root node: ";
    std::cin >> rootData;
    Node *root = new Node(rootData);

    // std::cout << "Enter the value for the left child of the root: ";
    int leftData;
    std::cin >> leftData;
    root->left = new Node(leftData);

    // std::cout << "Enter the value for the right child of the root: ";
    int rightData;
    std::cin >> rightData;
    root->right = new Node(rightData);

    // std::cout << "Enter the value for the left child of the left child: ";
    int leftLeftData;
    std::cin >> leftLeftData;
    root->left->left = new Node(leftLeftData);

    // std::cout << "Enter the value for the right child of the left child: ";
    int leftRightData;
    std::cin >> leftRightData;
    root->left->right = new Node(leftRightData);

    // std::cout << "Enter the value for the left child of the right child: ";
    int rightLeftData;
    std::cin >> rightLeftData;
    root->right->left = new Node(rightLeftData);

    // std::cout << "Enter the value for the right child of the right child: ";
    int rightRightData;
    std::cin >> rightRightData;
    root->right->right = new Node(rightRightData);

    // Calling the preorder function to perform Preorder Traversal
    preorder(root);

    // Free allocated memory
    delete root->left->right;
    delete root->left->left;
    delete root->left;
    delete root->right->right;
    delete root->right->left;
    delete root->right;
    delete root;

    return 0;
}

Test Case 1: Null Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 0 Enter the value for the right child of the root: 0 Enter the value for the left child of the left child: 0 Enter the value for the right child of the left child: 0 Enter the value for the left child of the right child: 0 Enter the value for the right child of the right child: 0

Explanation: In this case, a tree with only the root node is created. The output should be 1 as there are no left or right children.

Test Case 2: True Binary Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7

Explanation: This input creates a balanced binary tree. The output should be in the order

1 2 4 5 3 6 7 representing the preorder traversal.

Test Case 3: False Binary Tree

• Input:

Enter the value for the root node: 1 Enter the value for the left child of the root: 2 Enter the value for the right child of the root: 3 Enter the value for the left child of the left child: 4 Enter the value for the right child of the left child: 5 Enter the value for the left child of the right child: 6 Enter the value for the right child of the right child: 7 Enter the value for the left child of the left child of the left child: 8

Explanation: This input creates an unbalanced binary tree. The output should be in the order

1 2 4 5 3 6 7 8 representing the preorder traversal. This demonstrates that the code handles unbalanced trees as well.

STEP-BY-STEP EXPLAINATION

Step 1: Define a Node class

This class defines a simple binary tree node with an integer data, and pointers to its left and right children. The constructor initializes the data field with the provided value.

Step 2: Implement a Preorder Traversal Function

The preorder function is a recursive implementation of the Preorder Traversal algorithm. It takes a pointer to a Node (representing the root of a tree or subtree) and prints the data of the current node. It then recursively calls itself on the left and right subtrees.

Step 3: Implement the main function

• An instance of the Node class is created to represent the root of a binary tree with the value 10.
• Additional nodes are created to form a binary tree structure.
• The preorder function is called with the root of the tree (root) to perform a preorder traversal.

The output represents the result of the preorder traversal, showing the values of each node in the specified order.

TIME COMPLEXITY AND SPACE COMPLEXITY

The time and space complexity of preorder traversal in a binary tree depends on the number of nodes in the tree, denoted as "n.”

Time Complexity:

In preorder traversal, each node is visited exactly once. Therefore, the time complexity is O(n), where "n" is the number of nodes in the binary tree. This is because the algorithm must visit every node in the tree, and the work done at each node is constant.

Space Complexity:

The space complexity of preorder traversal is determined by the maximum depth of the function call stack during the recursive calls. In the worst case, the maximum depth of the stack is equal to the height of the binary tree. For a balanced binary tree, the height is log(n) (where "n" is the number of nodes), and for an unbalanced tree, it could be as bad as O(n) if the tree is skewed.

Therefore, in the worst case, the space complexity of preorder traversal is O(n), where "n" is the number of nodes in the binary tree. This accounts for the space used by the call stack during the recursive calls. In the average case, for a balanced binary tree, the space complexity is O(log n) due to the logarithmic height of the tree.

REAL WORLD APPLICATIONS OF PRE ORDER TRAVERSAL

Here are some real-world applications of preorder traversal:

HTML Document Parsing:

In web development, HTML documents are hierarchical structures. Preorder traversal can be applied to parse and process HTML documents, helping to extract information or manipulate the structure.

Database Indexing:

In databases, tree structures like B-trees and binary search trees are used for indexing. Preorder traversal can assist in navigating these structures for efficient retrieval of data.

AI Decision Trees:

In artificial intelligence, decision trees are used to model decision-making processes. Preorder traversal can assist in navigating these trees to make decisions based on given conditions.

Computer Graphics:

Hierarchical structures are common in computer graphics, especially in scenes composed of objects with parent-child relationships. Preorder traversal can be applied to efficiently process and render such scenes.

Robotics Path Planning:

For robotic systems navigating through a physical environment, the representation of the environment can be in the form of a tree. Preorder traversal can help in path planning and obstacle avoidance.

In these applications, the hierarchical nature of data lends itself well to tree traversal algorithms like preorder traversal. The ability to process data in a specific order is crucial for efficient and effective problem-solving in these domains.