Prefix Sum
PREFIX SUM
Arrays play a crucial role in the context of prefix sum calculations. The prefix sum algorithm operates on arrays, allowing for efficient computation of cumulative sums. By storing the elements of a sequence in an array, we can easily access and manipulate them during the prefix sum process.
When applying the prefix sum algorithm to an array, each element represents a value in the sequence. The sum at each index of the resulting prefix sum array corresponds to the cumulative sum of all preceding elements, including itself, in the original array. This provides a concise representation of the running sum up to each element.
Arrays offer several advantages in the context of prefix sum operations. They provide constant-time access to individual elements, allowing for efficient calculations and updates. Additionally, arrays facilitate the iterative nature of the prefix sum algorithm, as elements can be easily accessed and added to the running sum during each iteration.
INTRODUCTION
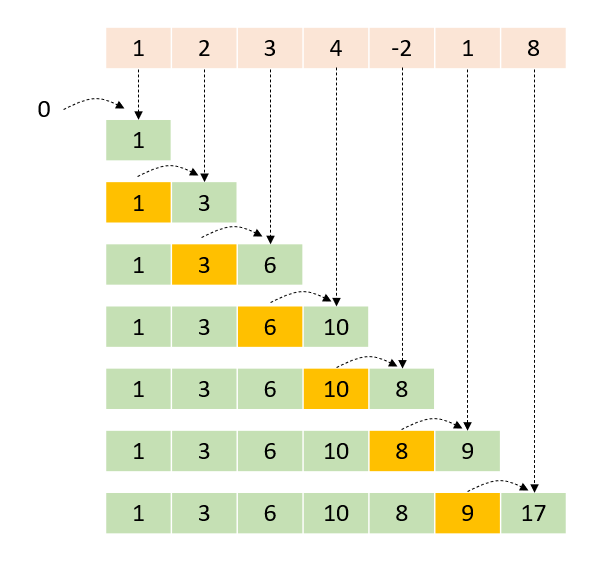
Prefix sum is a common operation in computer science and mathematics that involves calculating the cumulative sum of elements in an array or sequence. In other words, it computes the running sum of a sequence up to each element. The result is a new array or sequence where the value at each index is the sum of all preceding elements, including itself.
Prefix sum is often used as a building block for various algorithms and data structures. It can provide efficient solutions for problems such as range sum queries, finding the number of elements less than or equal to a given value, and many more.
The prefix sum algorithm works by iteratively adding the current element to the sum of all previous elements. This process can be performed efficiently in linear time, making it a valuable tool in many computational tasks.
Overall, prefix sum is a powerful technique that allows for efficient calculations of cumulative sums in arrays or sequences, enabling faster and more optimized solutions to various problems.
CODE
PYTHON
# Copyrights to venkys.io
# For more programs visit venkys.io
# Python program for PrefixSum
def prefixSum(arr):
# Iterate through the array starting from index 1
for i in range(1, len(arr)):
# Update each element by adding the value of the preceding element
arr[i] += arr[i - 1]
# Print the resulting array after the prefix sum calculation
print(*arr)
if __name__ == "__main__":
# Read input from stdin
input_str = input()
# Convert the input string to an array (list) of integers
arr = [int(num) for num in input_str.split()]
# Call the prefixSum function with the input array
prefixSum(arr)
Step-by-Step Explanation
1.Function Definition:
def prefixSum(arr):: This line defines a function named prefixSum that takes a list arr as its parameter.
2.Prefix Sum Calculation:
for i in range(1, len(arr)): This line initiates a for loop that iterates over the indices of the list arr, starting from 1 and going up to len(arr) - 1. arr[i] += arr[i - 1] This line updates each element of the list arr by adding the value of the preceding element (arr[i-1]). This process calculates the prefix sum, where each element represents the sum of all elements up to and including the current index.
3.Print Result:
print(*arr) This line prints the resulting list after the prefix sum calculation. The *arr syntax is used to unpack the list, so each element is printed separated by a space.
JAVA
// Copyrights to venkys.io
// For more programs visit venkys.io
// Java program for PrefixSum
import java.util.Scanner;
public class PrefixSum {
// Step 1: Define a class named PrefixSum
// Step 2: Define a method named prefixSum that takes an integer array as a parameter
public static void prefixSum(int[] arr) {
for (int i = 1; i < arr.length; i++) {
// Step 3: Iterate through the array starting from index 1
arr[i] += arr[i - 1];
// Step 4: Update each element in the array to be the sum of its current value and the previous element
}
for (int num : arr) {
// Step 5: Iterate through the updated array
System.out.print(num + " ");
// Step 6: Print each element followed by a space
}
System.out.println();
// Step 7: Print a new line after printing all elements
}
// Step 8: Define the main method
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// System.out.print("Enter the number of elements for the array: ");
int numElements = scanner.nextInt();
int[] arr = new int[numElements];
// Step 9: Create an integer array named arr with user-input values
// System.out.print("Enter the elements of the array separated by space: ");
for (int i = 0; i < numElements; i++) {
arr[i] = scanner.nextInt();
}
prefixSum(arr);
// Step 10: Call the prefixSum method with the array arr as an argument
}
}
Step-by-Step Explanation
1.Main Class:
Declares a Java class named Main. Contains a main method, which is the entry point of the program
2.prefixSum Method:
Static method within the Main class. Takes an array of integers (int[] arr) as a parameter. Returns an integer, representing the prefix sum of the array.
3.Prefix Sum Calculation:
The method iterates through the array starting from index 1, updating each element to be the sum of its current value and the previous element.
-
After updating the array, it iterates through the array again and prints each element followed by a space.
-
Print Result :
The main method creates an array, calls the prefixSum method, and prints the result.
CPP
// Copyrights to venkys.io
// For more programs visit venkys.io
// C++ program for PrefixSum
#include <iostream>
#include <vector>
// Function to calculate the prefix sum of a vector
void prefixSum(std::vector<int>& arr) {
// Iterate through the vector starting from index 1
for (int i = 1; i < arr.size(); ++i) {
// Update each element to be the sum of its current value and the previous element
arr[i] += arr[i - 1];
}
// Print the resulting vector after prefix sum calculation
for (int num : arr) {
std::cout << num << " ";
}
// Print a new line to separate the output
std::cout << std::endl;
}
// Main function
int main() {
// Read the number of elements from the user
// std::cout << "Enter the number of elements for the array: ";
int num_elements;
std::cin >> num_elements;
// Create a vector named arr with user-input values
std::vector<int> arr(num_elements);
// std::cout << "Enter the elements of the array separated by space: ";
for (int i = 0; i < num_elements; ++i) {
std::cin >> arr[i];
}
// Call the prefixSum function to calculate and print the prefix sum
prefixSum(arr);
// Return 0 to indicate successful execution
return 0;
}
Step-by-Step Explanation :
- #include and #include : These are header files for input/output and dynamic array (vector) handling in C++.
- void prefixSum(std::vector& arr): This declares a function named prefixSum that takes a reference to a vector of integers as a parameter.
- The logic inside prefixSum remains the same as in the Python version. It iterates through the vector, updating each element to be the sum of its current value and the previous element.
- The main function is similar to the Python version. It creates a vector named arr, initializes it with values 1, 2, 3, 4, 5, 6, calls the prefixSum function, and prints the result.
OUTPUT
The code prints the prefixsum of the array as result 1 3 6 10 15 21 separated by space.
Time and Space Complexity Analysis
Time Complexity: The time complexity of the prefix sum algorithm is O(n), where n is the number of elements in the array or vector. This is because the algorithm iterates through the entire array once, performing a constant-time operation (updating each element) at each step. The loop runs for (n - 1) iterations, so the overall time complexity is linear in terms of the input size.
Space Complexity: The space complexity of the code is O(n), where n is the number of elements in the array or vector. This is due to the storage of the array/vector itself. The algorithm doesn't use any additional data structures that scale with the input size. The space complexity is dominated by the input data structure.
Real-World Applications of PrefixSum
1.Image Processing:
Integral Images: In computer vision and image processing, prefix sums are used to efficiently calculate the sum of pixel values in rectangular regions of an image. This is commonly employed in tasks like object recognition and feature extraction.
2.Genomics:
DNA Sequence Matching: In genomics, particularly in bioinformatics, prefix sums are used in algorithms for efficient sequence matching and analysis. For example, it can be applied to find common subsequences or patterns in DNA sequences.
3.Data Analytics:
Running Totals and Aggregates: Prefix sums are useful in data analytics for calculating running totals, aggregates, or cumulative metrics in time-series data. This can provide insights into trends and patterns over time.
4.Game Development:
Pathfinding Algorithms: In game development, prefix sums can be used in pathfinding algorithms to efficiently calculate the cumulative cost of moving through a grid. This is crucial for determining optimal paths for characters or entities in a game.
Test Cases
Test Case 1: Input:
3 4 -2 6 -3 1
Output:
3 7 5 11 8 9
Explanation:
- The program takes the input array
[3, 4, -2, 6, -3, 1]. - It then computes the prefix sum of the array.
- The prefix sum is calculated as follows:
- The first element remains unchanged.
- For each subsequent element, it adds the value of the preceding element to itself.
- After calculating the prefix sum, the program prints the resulting array
[3, 7, 5, 11, 8, 9].
Test Case 2: Input:
-1 2 -3 4 -5 6 -7
Output:
-1 1 -2 2 -3 3 -4
Explanation:
- The program takes the input array
[-1, 2, -3, 4, -5, 6, -7]. - It then computes the prefix sum of the array.
- The prefix sum is calculated as follows:
- The first element remains unchanged.
- For each subsequent element, it adds the value of the preceding element to itself.
- After calculating the prefix sum, the program prints the resulting array
[-1, 1, -2, 2, -3, 3, -4].
