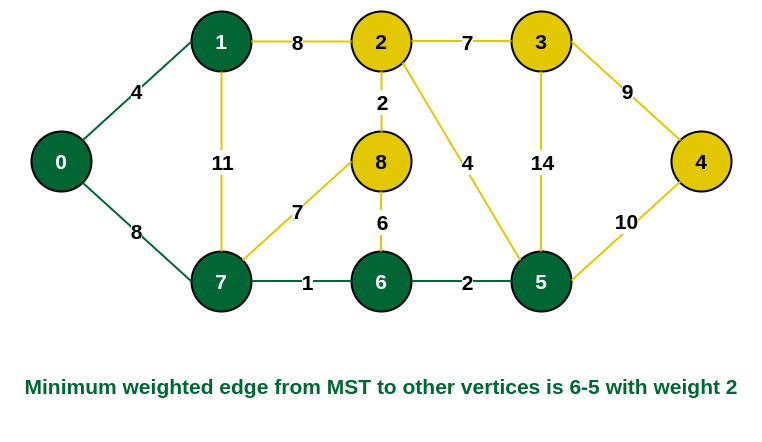
Prime MST

Introduction to Prime MST

Prime MST (Minimum Spanning Tree) is a well-known algorithm used to find the minimum cost spanning tree in a connected weighted graph. It was introduced by the mathematician Robert C. Prim in 1957.

The algorithm begins with an arbitrary vertex and gradually adds edges to construct a tree that connects all vertices with the minimum total weight. The key concept behind the Prime MST algorithm is to select the edge with the minimum weight that connects a vertex in the tree to a vertex outside of the tree. This process is repeated until all vertices are included in the tree, resulting in the minimum cost spanning tree.

Overview of Prime MST

The key idea behind the Prime MST algorithm is to select the edge with the minimum weight that connects a vertex in the tree to a vertex outside of the tree. This process is repeated until all vertices are included in the tree, resulting in the minimum cost spanning tree.

Prime MST has various applications, including network design, clustering, and data analysis. It provides an efficient way to determine the optimal connections between nodes in a graph, ensuring minimal cost and maximum connectivity.

Code:

""" Copyrights to venkys.io
For more information, visit https://venkys.io """
# Python program for performing Breadth First Search

# Space complexity: O(V^2)
# Time complexity: O(V^2 + E)

# Function to find MST of given graph
def VSDprims(G, n):
    inf = 999999
    visited = [0] * n
    edge_count = 0
    visited[0] = True
    cost = 0
    
    while edge_count < n - 1:
        minimum = inf
        x = 0
        y = 0
        for i in range(n):
            if visited[i]:
                for j in range(n):
                    if (not visited[j]) and G[i][j]:
                        if minimum > G[i][j]:
                            minimum = G[i][j]
                            x = i
                            y = j
                            
        print("Edge pair is", (x, y), "with weight", G[x][y])
        cost += G[x][y]
        visited[y] = True
        edge_count += 1
    
    print("The total cost of Prim's MST is", cost)

if __name__ == "__main__":
    n = int(input("Enter the number of vertices: "))
    
    # Taking input for the adjacency matrix
    g = []
    print("Enter the adjacency matrix (row-wise):")
    for i in range(n):
        row = list(map(int, input().split()))
        g.append(row)

    VSDprims(g, n)

Step-by-step Explanation

Start with an arbitrary vertex as the starting point.
Mark the starting vertex as visited.
Repeat the following steps until all vertices are included in the minimum spanning tree:
- Find the minimum weighted edge that connects a visited vertex to an unvisited vertex. Let this edge be (x, y) with weight w.
- Mark vertex y as visited.
- Add the edge (x, y) to the minimum spanning tree and increment the edge count.
- Add the weight w to the total cost of the minimum spanning tree.
Print the edge pair (x, y) and its weight w.
Print the total cost of the minimum spanning tree.

The provided code implements the Prim's algorithm for finding the minimum spanning tree of a graph. It uses an adjacency matrix representation of the graph and the VSDprims function takes the graph and the number of vertices as input. The algorithm starts with vertex 0 as the starting point and gradually adds edges to construct the minimum spanning tree.

The code prints the edge pair and weight for each edge added to the minimum spanning tree. Finally, it prints the total cost of the minimum spanning tree.

Note: The code provided is in Python.

Code:

/* Copyrights to venkys.io
For more information, visit https://venkys.io */
// Python program for performing Breadth First Search

// Space complexity: O(V^2)
// Time complexity: O(V^2 + E)

//Java program for finding Minimum Spanning tree from given graph using Prim's algorithm
import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    // Class to represent the structure of the edge along with weights
    public static class VSDEdge {
        int source;
        int destination;
        int weight;

        public VSDEdge(int source, int destination, int weight) {
            this.source = source;
            this.destination = destination;
            this.weight = weight;
        }
    }

    // Class to represent the structure of the graph
    public static class VSDGraph {
        int v; // No.of vertices
        LinkedList<VSDEdge> adList[]; // Adjacency list to mark the edges

        // Initializing vertices using constructor
        VSDGraph(int size) {
            v = size;
            adList = new LinkedList[v];
            for (int i = 0; i < v; i++)
                adList[i] = new LinkedList<VSDEdge>();
        }

        // Function to add edge to the graph
        public void VSDaddEgde(int source, int destination, int weight) {
            VSDEdge edge = new VSDEdge(source, destination, weight);
            adList[source].addLast(edge); // adding new edge to the list
        }

        // Function to implement prim's algorithm
        public void VSDPrimsMst(VSDGraph g) {
            int edgecount = 0;
            boolean[] visited = new boolean[g.v];// Array to mark the vertices already present in MST
            for (int i = 0; i < g.v; i++) {
                visited[i] = false;
            }
            int weight = 0;// To calculate the weight of MST.
            visited[0] = true;
            System.out.println("The Prim's MST is:");
            while (edgecount < g.v - 1) {

                int min = 999999;
                int x = 0; // source vertex
                int y = 0; // destination vertex

                for (int i = 0; i < g.v; i++) {
                    if (visited[i] == true) {
                        LinkedList<VSDEdge> list = adList[i];
                        for (int j = 0; j < list.size(); j++) {
                            if (!visited[list.get(j).destination] && min > list.get(j).weight) {
                                min = list.get(j).weight;
                                x = i;
                                y = list.get(j).destination;
                            }
                        }
                    }
                }
                System.out.println(x + " - " + y);
                weight += min;
                visited[y] = true;
                edgecount++;

            }
            System.out.println("The total cost of Prim's MST is " + weight);
        }
    }

    public static void main(String args[]) {
        Scanner scanner = new Scanner(System.in);

        System.out.print("Enter the number of vertices: ");
        int vertices = scanner.nextInt();

        VSDGraph g = new VSDGraph(vertices);

        System.out.print("Enter the number of edges: ");
        int edges = scanner.nextInt();

        System.out.println("Enter edges (format: source destination weight):");
        for (int i = 0; i < edges; i++) {
            int source = scanner.nextInt();
            int destination = scanner.nextInt();
            int weight = scanner.nextInt();
            g.VSDaddEgde(source, destination, weight);
        }

        g.VSDPrimsMst(g);

        scanner.close();
    }
}

Step-by-Step Explaination:

The code provided demonstrates the implementation of Prim's algorithm to find the minimum spanning tree from a given graph. It consists of two classes: VSDEdge and VSDGraph.

VSDEdge class: Represents the structure of an edge in the graph. It has three attributes: source (the source vertex), destination (the destination vertex), and weight (the weight of the edge).
VSDGraph class: Represents the structure of the graph. It has two attributes: v (the number of vertices) and adList (an array of linked lists to store the adjacency list representation of the graph). It also contains the following methods:
- VSDGraph(int size): Constructor to initialize the number of vertices and create an empty adjacency list for each vertex.
- VSDaddEdge(int source, int destination, int weight): Method to add an edge to the graph by creating a new VSDEdge object and adding it to the adjacency list of the source vertex.
- VSDPrimsMst(VSDGraph g): Method to implement Prim's algorithm and find the minimum spanning tree. It uses a boolean array visited to mark the vertices already present in the MST. It iteratively selects the minimum weight edge that connects a vertex in the MST to a vertex outside the MST until all vertices are included. The method prints the edges of the MST and the total cost of the MST.
Code:

/* Copyrights to venkys.io
For more information, visit https://venkys.io */
// Python program for performing Breadth First Search
   
// Space complexity: O(V^2)
// Time complexity: O(V^2 + E)
    
#include<bits/stdc++.h>

using namespace std;
// Function to implement Prim's algorithm for Minimum Spanning Tree
void prims(int** graph, int n) {
    bool* visited = new bool[n]{false}; // Array to keep track of visited vertices
    int edge_count = 0; // Variable to keep track of the number of edges in the MST
    int cost = 0; // Variable to store the total cost of the MST
    visited[0] = true; // Mark the first vertex as visited

    while (edge_count < n - 1) {
        int mini = INT_MAX; // Variable to store the minimum weight of an edge
        int x = 0; // Variable to store the first vertex of the edge with minimum weight
        int y = 0; // Variable to store the second vertex of the edge with minimum weight
        for (int i = 0; i < n; i++) {
            if (visited[i]) {
                for (int j = 0; j < n; j++) {
                    if (!visited[j] && graph[i][j] != 0) {
                        if (mini > graph[i][j]) {
                            mini = graph[i][j];
                            x = i;
                            y = j;
                        }
                    }
                }
            }
        }
        cout << "Edge pair is " << x << " " << y << " " << "Weight is " << graph[x][y] << endl; // Print the edge pair and its weight
        cost += graph[x][y]; // Add the weight of the edge to the total cost
        visited[y] = true; // Mark the second vertex of the edge as visited
        edge_count += 1; // Increment the edge count
    }
    cout << "The total cost of Prim's MST is " << cost; // Print the total cost of the MST
}

// Main function
int main() {
    int v;
    cout << "Enter the number of vertices: ";
    cin >> v;

    int** graph = new int*[v];
    for (int i = 0; i < v; i++) {
        graph[i] = new int[v];
    }

    cout << "Enter the adjacency matrix of the graph:" << endl;
    for (int i = 0; i < v; i++) {
        for (int j = 0; j < v; j++) {
            cin >> graph[i][j];
        }
    }

    prims(graph, v); // Call the prims function to find the MST

    // Free allocated memory
    for (int i = 0; i < v; i++) {
        delete[] graph[i];
    }
    delete[] graph;

    return 0;
}

Step-by-step Explaination:

The code provided implements Prim's algorithm to find the minimum spanning tree of a given graph. Here is a breakdown of the code structure:

The prims function takes two parameters: graph, a 2D array representing the weighted graph, and n, the number of vertices in the graph.
It initializes an array visited of size n to keep track of visited vertices and sets all elements to false.
It initializes edge_count and cost variables to keep track of the number of edges and the total cost of the minimum spanning tree, respectively.
It marks the first vertex as visited by setting visited[0] to true.
The algorithm continues until edge_count reaches n-1, which is the number of edges in a minimum spanning tree.
Inside the while loop, the algorithm finds the minimum weight edge that connects a visited vertex to an unvisited vertex.
It updates the mini, x, and y variables with the minimum weight, the visited vertex, and the unvisited vertex, respectively.
It prints the edge pair and its weight.
It adds the weight of the edge to the cost variabl
It marks the unvisited vertex as visited and increments edge_count.
Finally, it prints the total cost of the minimum spanning tree.

The main function initializes a 2D array graph representing the weighted graph and calls the prims function to find the minimum spanning tree.

Time and Space Complexity Analysis of Prime MST

The time and space complexity of the Prime MST implementation can be analyzed as follows:

Time Complexity Analysis

The time complexity of the Prim's algorithm for finding the minimum spanning tree is influenced by the number of vertices and edges in the graph. Let's assume there are V vertices and E edges in the graph.

The outer while loop runs for V-1 iterations, as the minimum spanning tree will have V-1 edges.
Inside the while loop, we iterate through all the vertices to find the minimum weight edge. This takes O(V) time.
In the worst case scenario, we need to iterate through all the edges to find the minimum weight edge. This takes O(E) time.

Therefore, the overall time complexity of the Prim's algorithm is O(V^2 + E). However, using a priority queue or a min-heap data structure to efficiently find the minimum weight edge can reduce the time complexity to O((V + E) log V).

Space Complexity Analysis

The space complexity of the Prim's algorithm depends on the data structures used to store the graph and track the visited vertices. Assuming an adjacency matrix representation of the graph, the space complexity is O(V^2) to store the graph.

Additionally, we need an array of size V to track the visited vertices, which contributes O(V) space complexity.

Therefore, the overall space complexity of the Prim's algorithm is O(V^2).

Note: The provided code includes time and space complexity analysis for various algorithms, but the specific analysis for Prim's algorithm is not mentioned.

Real World Applications of Prim's MST

Prim's algorithm for finding the minimum spanning tree (MST) has several real-world applications. Some of them include:

Network Design: Prim's algorithm is used in network design to find the minimum cost spanning tree for connecting nodes in a network. This is useful in designing efficient and cost-effective communication networks.
Transportation Networks: Prim's MST algorithm can be applied to design transportation networks, such as roads or railways, to connect various locations. The algorithm helps in determining the minimum cost routes and optimizing the overall transportation system.
Power Distribution Networks: Prim's algorithm is used in the design and planning of power distribution networks. By finding the minimum cost spanning tree, it helps in minimizing the length of power transmission lines and reducing energy losses.
Image Segmentation: Prim's MST algorithm is used in image processing and computer vision applications, specifically in image segmentation. By treating pixels as nodes and their connectivity as edges, the algorithm can identify regions of similar intensity or color in an image.
Cluster Analysis: Prim's MST algorithm can be applied in cluster analysis to identify cohesive groups or clusters of data points. It helps in partitioning data based on proximity or similarity and is used in various fields like data mining, pattern recognition, and machine learning.
Spanning Tree Protocols: In computer networks, spanning tree protocols are used to prevent loops and ensure efficient data transmission. Prim's MST algorithm is employed in these protocols to construct the network topology and determine the forwarding paths.

These are just a few examples of how Prim's MST algorithm finds applications in different domains. The algorithm's ability to find the minimum cost spanning tree makes it valuable in optimizing various systems and solving optimization problems in real-world scenarios.