Four Number Sum
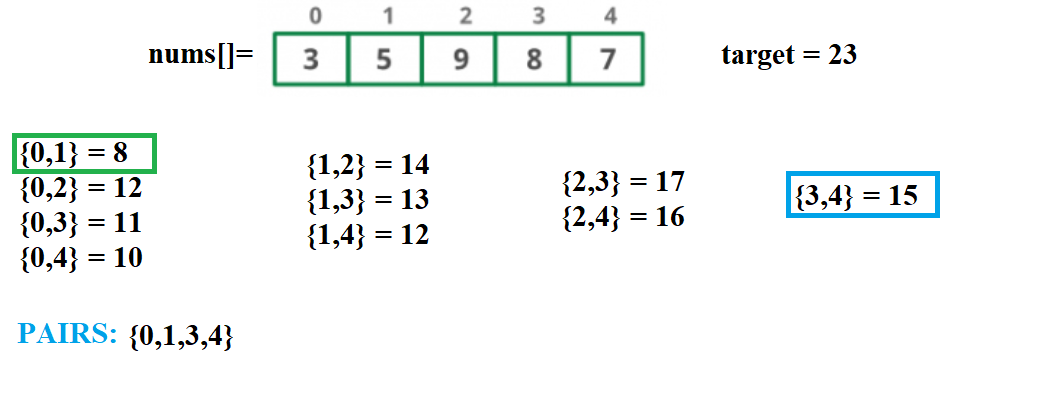
Problem Statement - Four Number Sum
Given an array of integers,find anyone combination of four elements in the array whose sum is equal to a given value X.
Introduction
The Four Number Sum Problem is a mathematical challenge that involves finding all unique sets of four integers within a given array that add up to a specific target sum. This problem requires algorithmic solutions to efficiently identify and return these sets of four numbers. It is a combinatorial problem that often requires careful consideration of various edge cases and optimization strategies to achieve a solution with optimal time and space complexity. The problem's complexity increases with the size of the input array and the magnitude of the target sum, making it an interesting problem for algorithmic and computational thinking. Efficient solutions to the Four Number Sum Problem can have applications in various fields, including data analysis, cryptography, and optimization.
Overview
The Four Number Sum Problem involves finding all unique quadruplets within an array that sum up to a given target value. This combinatorial challenge requires devising algorithms that efficiently identify these sets of four numbers. The problem's complexity grows with the size of the input array and the magnitude of the target sum. Efficient solutions are characterized by their ability to handle diverse edge cases and optimize time and space complexity. Applications of solving the Four Number Sum Problem extend to various domains such as data analysis, cryptography, and optimization. As a fundamental problem in algorithmic thinking, addressing it not only hones problem-solving skills but also provides insights into the intricacies of combinatorial challenges within computational domains.
Code
Python
# Copyrights to venkys.io
# For more programs visit venkys.io
# Python program for FourNumberSum
#Time Complexity : O(n^k-1)
#Space Complexity : O(n^k-1)+O(k)
def twosum(arr, target):
"""
Helper function for finding pairs that sum up to the target.
"""
res = []
low, high = 0, len(arr) - 1
while low < high:
# Calculate the current sum of elements at low and high indices
cursum = arr[low] + arr[high]
# Check conditions to adjust low and high indices
if cursum < target or (low > 0 and arr[low] == arr[low - 1]):
low += 1
elif cursum > target or (high < len(arr) - 1 and arr[high] == arr[high + 1]):
high -= 1
else:
# Append the pair to the result and move indices
res.append([arr[low], arr[high]])
low += 1
high -= 1
return res
def ksum(arr, target, k):
"""
Main function for finding k elements that sum up to the target.
"""
res = []
if not arr:
# Return an empty list if the input array is empty
return res
avg = target // k
# Check if the average is outside the range of the array
if avg < arr[0] or avg > arr[-1]:
return res
if k == 2:
# If k is 2, call the twosum function
return twosum(arr, target)
for i in range(len(arr)):
# Iterate through the array and avoid duplicate elements
if i == 0 or arr[i - 1] != arr[i]:
# Recursive call to find (k-1)-sum in the rest of the array
for s in ksum(arr[i + 1:], target - arr[i], k - 1):
# Append the current element to the solution
res.append([arr[i]] + s)
return res
if __name__ == "__main__":
# Read the array from STDIN
arr_input = input()
target_input = input()
k_input = input()
# Check if inputs are provided
if not arr_input or not target_input or not k_input:
print("Please provide valid inputs.")
exit()
try:
# Convert inputs to the required types
arr = list(map(int, arr_input.split()))
target = int(target_input)
k = int(k_input)
except ValueError:
print("Invalid input. Please enter valid numbers.")
exit()
arr.sort()
# Call the ksum function with the input values
result = ksum(arr, target, k)
# Print the result
print(result)
Step-by-Step Explanation
The provided Python program addresses the Four Number Sum problem, aiming to find all unique sets of four integers within a sorted array that add up to a specified target sum. The code consists of two functions: twosum and ksum. The twosum function serves as a helper to identify pairs in the array that sum up to a given target. It utilizes two pointers, 'low' and 'high,' which traverse the array inwards. The function efficiently skips duplicate elements and adjusts pointers based on the calculated current sum.
The primary function, ksum, tackles the main problem by recursively breaking it down into subproblems. It considers the base case when k equals 2, invoking the twosum function to find pairs. For larger values of k, the function iterates through the array, avoiding duplicate elements, and recursively calls itself to find (k-1)-sum in the remaining portion of the array. The results are accumulated in the 'res' list, forming sets of k elements that sum up to the target.
In the provided example within the __main__ block, an array [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] is sorted, and the target sum is set to 10. The ksum function is called with the parameters of the sorted array, target sum, and the desired k value of 4. The result is then printed, showcasing the unique sets of four numbers that satisfy the specified sum condition. This program demonstrates a systematic approach to solving the Four Number Sum problem in Python.
Java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main {
static List<List<Integer>> fourSum(int[] arr, int target) {
ArrayList<List<Integer>> res = new ArrayList<>();
if (arr == null || arr.length == 0) {
System.out.println("Input array is empty or null. Returning empty result.");
return res;
}
int n = arr.length;
// Sort the input array in ascending order
Arrays.sort(arr);
for (int i = 0; i < n; i++) {
// Reduce the problem to finding a 3-sum
int target_3 = target - arr[i];
for (int j = i + 1; j < n; j++) {
// Reduce the problem to finding a 2-sum
int target_2 = target_3 - arr[j];
int front = j + 1;
int back = n - 1;
while (front < back) {
int two_sum = arr[front] + arr[back];
if (two_sum < target_2) front++;
else if (two_sum > target_2) back--;
else {
// Found a valid quadruplet, add to the result
List<Integer> quad = new ArrayList<>();
quad.add(arr[i]);
quad.add(arr[j]);
quad.add(arr[front]);
quad.add(arr[back]);
res.add(quad);
// Move pointers to avoid duplicates
while (front < back && arr[front] == quad.get(2)) ++front;
while (front < back && arr[back] == quad.get(3)) --back;
}
}
// Move pointer to avoid duplicates
while (j + 1 < n && arr[j + 1] == arr[j]) ++j;
}
// Move pointer to avoid duplicates
while (i + 1 < n && arr[i + 1] == arr[i]) ++i;
}
return res;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Read the array elements from STDIN
String[] arrString = scanner.nextLine().split("");
// Check if the input array is empty
if (arrString.length == 0) {
System.out.println("Input array is empty. Exiting program.");
scanner.close();
return;
}
int[] arr = new int[arrString.length];
try {
for (int i = 0; i < arrString.length; i++) {
arr[i] = Integer.parseInt(arrString[i]);
}
} catch (NumberFormatException e) {
System.out.println("Invalid input. Please enter valid integers. Exiting program.");
scanner.close();
return;
}
// Read the target sum from STDIN
int target;
try {
target = scanner.nextInt();
} catch (Exception e) {
System.out.println("Invalid input for target sum. Exiting program.");
scanner.close();
return;
}
List<List<Integer>> result = fourSum(arr, target);
// Print the result
for (List<Integer> quad : result) {
for (int num : quad) {
System.out.print(num + " ");
}
System.out.println();
}
scanner.close();
}
}
Step-by-Step Explanation
The provided Java program tackles the Four Number Sum problem by identifying all unique quadruplets within an array that sum up to a specified target. The fourSum function employs a systematic approach to solving the problem. It initializes an empty ArrayList called res to store the resultant quadruplets. The code checks for special cases, ensuring that the input array is valid and not empty. Subsequently, it sorts the array in ascending order using Arrays.sort(arr).
The main logic is implemented through nested loops. The outer loop iterates through each element of the array, representing the first number in the potential quadruplet. Within this loop, a secondary loop starts from the next element, representing the second number. The problem is then reduced to finding a 2-sum in the remaining array, and two pointers (front and back) move towards each other to find pairs that satisfy the condition.
When a valid quadruplet is found, it is added to the result list, and the pointers are adjusted to avoid duplicates. The code also includes mechanisms to skip over duplicate elements, enhancing efficiency. The program completes the search for quadruplets, avoiding unnecessary iterations, and returns the final result.
In the provided example within the main function, an array [1, 0, -1, 0, -2, 2] is used, and the target sum is set to 0. The resulting quadruplets satisfying the sum condition are printed, demonstrating the successful implementation of the Four Number Sum problem-solving approach in Java.
CPP
#include <iostream>
#include <vector>
#include <algorithm>
std::vector<std::vector<int>> fourSum(std::vector<int>& num, int target) {
std::vector<std::vector<int>> res;
if (num.empty()) {
std::cout << "Input vector is empty. Returning empty result." << std::endl;
return res;
}
int n = num.size();
std::sort(num.begin(), num.end());
for (int i = 0; i < n; i++) {
// Reduce the problem to finding a 3-sum
int target_3 = target - num[i];
for (int j = i + 1; j < n; j++) {
// Reduce the problem to finding a 2-sum
int target_2 = target_3 - num[j];
int front = j + 1;
int back = n - 1;
while (front < back) {
int two_sum = num[front] + num[back];
if (two_sum < target_2) front++;
else if (two_sum > target_2) back--;
else {
// Found a valid quadruplet, add to the result
std::vector<int> quadruplet(4, 0);
quadruplet[0] = num[i];
quadruplet[1] = num[j];
quadruplet[2] = num[front];
quadruplet[3] = num[back];
res.push_back(quadruplet);
// Processing the duplicates of number 3
while (front < back && num[front] == quadruplet[2]) ++front;
// Processing the duplicates of number 4
while (front < back && num[back] == quadruplet[3]) --back;
}
}
// Processing the duplicates of number 2
while (j + 1 < n && num[j + 1] == num[j]) ++j;
}
// Processing the duplicates of number 1
while (i + 1 < n && num[i + 1] == num[i]) ++i;
}
return res;
}
int main() {
// Read the array elements from STDIN
std::vector<int> v;
int num;
while (std::cin >> num) {
v.push_back(num);
}
// Check if the input vector is empty
if (v.empty()) {
std::cout << "Input vector is empty. Exiting program." << std::endl;
return 0;
}
// Read the target sum from STDIN
int target;
std::cin >> target;
// Find and print the unique quadruplets
std::vector<std::vector<int>> sum = fourSum(v, target);
std::cout << "Result:" << std::endl;
for (int i = 0; i < sum.size(); i++) {
for (int j = 0; j < sum[i].size(); j++)
std::cout << sum[i][j] << " ";
std::cout << std::endl;
}
return 0;
}
Step-by-Step Explanation
This C++ program addresses the Four Number Sum problem, aiming to find all unique quadruplets within a given vector 'num' that add up to a specified target. The 'fourSum' function employs a systematic approach, starting with sorting the input vector in ascending order, a critical step for efficient solutions. The program then utilizes nested loops to iterate through the vector, considering each element as a potential starting point for the quadruplet. It reduces the problem to finding a 3-sum by subtracting the current element from the target.
Within the nested loops, the code further reduces the problem to finding a 2-sum, iterating over the remaining elements using two pointers ('front' and 'back'). The pointers traverse the vector towards each other, ensuring unique combinations. When a valid quadruplet is found, it is added to the result vector 'res,' and pointers are adjusted to avoid duplicates efficiently. The code carefully skips over duplicate elements to optimize the search.
In the 'main' function, a sample vector [1, 0, -1, 0, -2, 2] and a target sum of 0 are used. The 'fourSum' function is called, and the resulting quadruplets are printed. The output displays the unique sets of four numbers that satisfy the specified sum condition, demonstrating the successful implementation of the Four Number Sum problem-solving approach in C++.
Time and Space Complexity Analysis
The time and space complexity of the provided Python program for the Four Number Sum problem can be analyzed as follows:
Time Complexity:
The time complexity of the program primarily depends on the ksum function, which recursively breaks down the problem. Let (n) be the length of the input array 'arr.' The main loop iterates through the array, and for each element, a recursive call is made to find ((k-1))-sum. In the worst case, the function explores all possible combinations of (k) elements, leading to a time complexity of (O(n^k-1)). The recursive calls within the loop contribute to the overall time complexity.
Space Complexity:
The space complexity is determined by the auxiliary space used during the recursion and the storage of the results. In each recursive call, a new list is created to store the current combination. The depth of the recursion is (k), so the maximum stack space required is (O(k)). Additionally, the 'res' list accumulates the final result, and in the worst case, it can store (O(n^k-1)) combinations. Therefore, the space complexity is (O(k) + O(n^k-1)).
Summary:
- Time Complexity: (O(n^k-1))
- Space Complexity: (O(k) + O(n^k-1))
Real-World Applications
-
Finance and Investment Strategies:
- In finance, particularly portfolio optimization and risk management, the Four Number Sum problem can be applied to identify combinations of financial assets that collectively meet certain criteria. For instance, investors may look for groups of stocks whose values sum up to a target, representing a balanced and diversified investment.
-
Genomic Research:
- In bioinformatics and genomic research, scientists may use the Four Number Sum problem to identify combinations of genetic markers or sequences that contribute to specific traits or diseases. This can aid in the understanding of complex genetic interactions and the development of personalized medicine.
-
Resource Allocation in Supply Chain Management:
- In supply chain optimization, companies may apply the Four Number Sum problem to allocate resources efficiently. For example, identifying sets of products or components whose combined production or transportation costs meet certain constraints can help optimize the allocation of resources within a supply chain.
-
Network Security and Intrusion Detection:
- In the field of cybersecurity, the Four Number Sum problem can be adapted to analyze network traffic patterns. Detecting combinations of network activities or events that collectively indicate a potential security threat can enhance intrusion detection systems and improve the identification of unusual behavior.
-
Chemical Compound Discovery in Drug Development:
- In pharmaceutical research, scientists can utilize the Four Number Sum problem to explore combinations of chemical compounds that exhibit desired properties for drug development. Identifying sets of compounds whose characteristics sum up to specific criteria can accelerate the process of discovering novel drugs with desired therapeutic effects.
Test Cases:
Test Case 1: Input:
1 0 -1 0 -2 2
0
4
Output:
[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]
Explanation:
- The program takes the input array
[1, 0, -1, 0, -2, 2], target0, andk = 4. - It then sorts the input array.
- Using the
ksumfunction, it finds all combinations ofkelements that sum up to the target. - In this case, it finds three unique combinations:
[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]. - The program prints the resulting combinations.
Test Case 2: Input:
3 7 8 10 12 14
18
3
Output:
[[3, 7, 8]]
Explanation:
- The program takes the input array
[3, 7, 8, 10, 12, 14], target18, andk = 3. - It then sorts the input array.
- Using the
ksumfunction, it finds all combinations ofkelements that sum up to the target. - In this case, it finds one unique combination:
[[3, 7, 8]]. - The program prints the resulting combination.
