Exploring Sorting Algorithms:

Sorting algorithms are a fundamental part of programming. They are algorithms that rearrange the elements of a collection (such as an array or a list) into a specified order, typically in ascending or descending numerical or lexicographical (alphabetical) order. Sorting is a common operation in many real-world applications, and efficient sorting algorithms are crucial for optimizing the performance of various computer programs. The choice of a sorting algorithm depends on factors such as the size of the data, the nature of the data, and the application’s specific requirements.

Introduction to Radix Sort:

Radix sort is a non comparitive integer sorting algorithm.

A non-comparitive integer sorting algorithm is an algorithm that sorts integers without explicitly comparing them to each other based on magnitude. Traditional sorting algorithms such as quicksort or merge sort, rely on comparisons between elements to establish their order. Non-comparitive integer sorting algorithms, on the other hand, use specific properties of integers to achieve sorting without direct comparisons. Few examples of non-comapritive integer sorting algorithms are Counting sort, Radix sort, Bucket Sort, Pigeonhole Sort and Flash Sort.

How does Radix Sort algorithms sorts numbers?

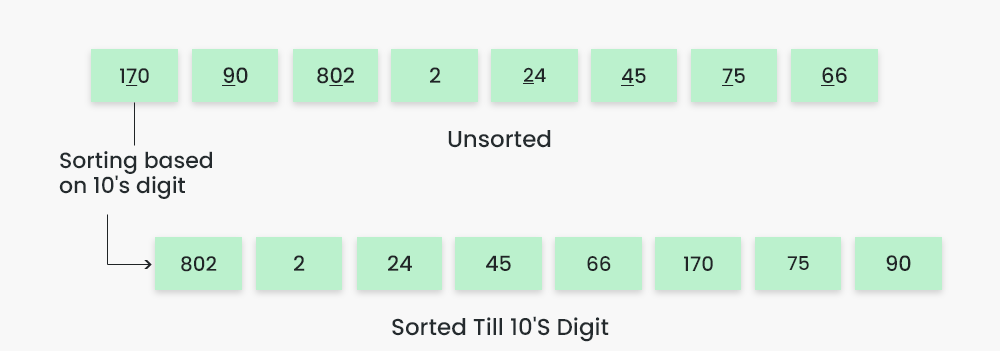
This algorithm sorts numbers by processing individual digits. It sorts the numbers by examining the digits from the least significant digit (LSD) to most significant digit (MSD) or vice versa. In simple words, in a array of integers, it first sorts the numbers basing on their one’s digit placed numbers followed by sorting based on 10’s digit placed numbers and then hundreds and so on.

How is Radix Sort different from Bucket Sort?

Radix sort and bucket sort are almost equivalent; bucket sort goes from MSD to LSD, while radix sort is capable of both "direction" (LSD or MSD).

Brief Explanation of Radix Sort Algorithm:

Identify the Maximum Element: Find the maximum value in the input array. This is needed to determine the number of digits in the largest element, which will determine the number of iterations needed to fully sort the array. For example in an array [10, 178, 827, 9, 12, 73] the largest element is 827 which has 3 digits. This gives us the idea that we need to sort the digits first in units place followed by tens place and then in hundreds place. On the other hand in arrays like [10, 2, 18, 9, 11] we just need to sort two times, First in unit digit and then in 10’s digit.
Initialize Exponential Value: Set the initial value of the exponent (exp) to 1, representing the least significant digit position.
Iterate Through Digits: While the maximum value divided by the exponent is greater than 0, perform the following steps for each iteration:
- Counting Sort: Use counting sort as a subroutine to sort the elements based on the current digit (specified by the exponent).
  - Count the frequency of each digit at the specified position, and then modify the count array to represent the position of elements in the output array.
- Update Exponential Value: Multiply the exponent by 10 to move to the next significant digit position.
Output Sorted Array: Once all iterations are complete, the array is fully sorted based on the individual digits of the elements.

Understanding how counting sort works

This sort works by counting the number of objects that have distinct key values, and using arithmetic to determine the position of each key in the output sequence.

Counting the Frequency
Determining Positions
Building the Output Array

Understanding Counting sort with the help of an example:

Let's consider an array of 5 values for our example: [4, 2, 4, 1, 3].

Identifying the range of input: First, we identify the range of the input. In our case, the input values range from 1 to 4.
Counting the frequency of each element: We count the frequency of each element in the input array and store it in a separate count array:

Input array: [4, 2, 4, 1, 3] Count array: [1, 1, 1, 2]

Here, the count array indicates that there is 1 occurrence of 1, 1 occurrence of 2, 1 occurrence of 3, and 2 occurrences of 4 in the input array.
Calculating the positions: We calculate the positions of each element in the output array based on the count array.

Count array: [1, 1, 1, 2] Cumulative count array: [1, 2, 3, 5]

The cumulative count array gives us the positions of each element in the sorted output array. For example, the value 1 will be at position 1, the value 2 will be at position 2, the value 3 will be at position 3, and the value 4 will be at positions 4 and 5 in the output array.

Creating the sorted array: Finally, we use the positions from the cumulative count array to place the elements in their sorted positions in the output array.

Output array: [1, 2, 3, 4, 4]

Performance of Radix Sort Algorithm

worst case time complexity of radix sort is O(n^2)

Best case time complexity of radix sort is O(a*n)

Average case time complexity of radix sort is O(p*(n+d))

Space complexity of radix sort is O(n+k)

Advantages of Radix Sort:

Linear Time Complexity: Radix sort has a time complexity of O(d * (n + k)), where n is the number of elements, k is the range of input values, and d is the number of digits in the maximum value. In many cases, the time complexity simplifies to O(n + k), making it a linear-time sorting algorithm.
Non-Comparison Based: Unlike comparison-based sorting algorithms (e.g., quicksort, mergesort), radix sort does not rely on comparison operations to arrange elements. Instead, it sorts based on the individual digits or significant places within the numbers, resulting in potentially faster performance for certain types of data.
Stable Sorting: Radix sort is a stable sorting algorithm, meaning it maintains the relative order of elements with equal keys. This property is often valuable when the original ordering of equivalent elements needs to be preserved.
Effective for Large Data Sets: Radix sort can be particularly effective for large data sets, especially when the range of input values is significantly smaller than the number of elements. It can outperform comparison-based sorting algorithms in such scenarios.

Disadvantages of Radix Sort:

Space Complexity: Radix sort requires additional space to hold the intermediate sorting results during each iteration. The space complexity is not constant and is dependent on the input size, which can be a drawback when working with very large data sets.
Limited Applicability: Radix sort is most effective for sorting integers or fixed-length strings with a limited range of values. However, it is not suitable for sorting arbitrary data structures or variable-length strings.
Not In-Place: Radix sort is not an in-place sorting algorithm, as it needs auxiliary space for intermediate results. This can be a drawback in situations where memory usage is a critical concern.
Complexity with Variable-Length Keys: When dealing with variable-length keys (e.g., strings of varying lengths), radix sort may become less efficient due to the need for additional processing to handle varying key lengths.
Limited to Positive Integers: Traditional radix sort algorithms are primarily intended for sorting positive integers and may require modifications to support sorting of negative numbers and floating-point numbers.

Real World Scenarios of Radix Sort:

Computer Graphics: In computer graphics, radix sort is used for various tasks, including depth buffering, which is crucial for rendering scenes accurately. The z-buffer, used for hidden surface removal, can be efficiently implemented using radix sort due to its stable sorting nature, ensuring that the relative depth ordering of objects is preserved.
String Sorting: While radix sort is primarily designed for integers, it can also be adapted for sorting fixed-length strings. It finds applications in databases or file systems for sorting strings with fixed lengths, such as sorting file names or database records based on specific index keys. This use case leverages the non-comparison based approach of radix sort for efficient string sorting.
Data Sorting in External Memory: Radix sort's I/O efficiency makes it suitable for sorting large datasets in external memory systems such as external hard drives or distributed file systems. Its linear time complexity and minimal disk seeks make it a desirable choice for sorting vast amounts of data that cannot fit entirely in main memory.
Network Routing: In networking, radix sort can be applied for IP address lookups in routing tables. The sorting of IP addresses helps in efficiently routing network traffic by quickly accessing the relevant routing information based on the destination IP address. The stable nature of radix sort is particularly beneficial in this context.
Data Compression: Radix sort is used as a crucial part of various data compression algorithms. For example, in Burrows-Wheeler Transform (BWT) based compression algorithms, the sorting step uses variants of radix sort to accomplish reordering and grouping of characters, leading to improved compression ratios and faster encoding/decoding.

Code in Python :

'''Copyrights to venkys.io
For more information, visite https://venkys.io"/

Python program to sort a given array in order using radix sort algorithm.'''

# Stable : Yes
# Inplace : Yes
# Adaptive : No

# Space complexity: O(n+k) where
  # n = number of elements in the input array
  # k = range of input values (number of unique digits)

#Time Complexity: O(d*(n+k)) /O(n+k) in simplified version
  # n=no. of elements
  # k= range of input values
  # d= no. of digits in maximum value

"""
    Perform counting sort on the array based on the given exponent.

    Parameters:
    arr (list): The input list to be sorted.
    exp (int): The exponent used for counting sort.

    Returns:
    None. Modifies the input array in-place.
    """
def counting_sort(arr, exp):
    n = len(arr)
    # Initialize an output array with zeros
    output = [0] * n
    # Initialize a count array to store the count of occurrences for each digit (0 to 9)
    count = [0] * 10

    # Count occurrences of each digit based on the given exponent
    for i in range(n):
        index = arr[i] // exp
        count[index % 10] += 1

    # Modify the count array to store the cumulative count of occurrences
    for i in range(1, 10):
        count[i] += count[i - 1]

    # Build the output array using the count information
    i = n - 1
    while i >= 0:
        index = arr[i] // exp
        output[count[index % 10] - 1] = arr[i]
        count[index % 10] -= 1
        i -= 1

    # Copy the sorted elements from the output array to the original array
    for i in range(n):
        arr[i] = output[i]

"""
    Perform radix sort on the given array.

    Parameters:
    arr (list): The input list to be sorted.

    Returns:
    list: The sorted array.
    """
def radix_sort(arr):
    # Find the maximum number in the array to determine the number of digits in it
    max_num = max(arr)
    # Initialize the exponent (exp) to the least significant digit
    exp = 1
    # Loop until all digits are processed, from the least significant to the most significant
    while max_num // exp > 0:
        # Call the counting_sort function to sort the array based on the current exponent
        counting_sort(arr, exp)
        # Move to the next significant digit by multiplying the exponent by 10
        exp *= 10
    # Return the sorted array
    return arr

def main():
    try:
        arr = list(map(int, input("Enter the elements of the array separated by space: ").split()))
        # Check if the array is empty, and raise a ValueError if it is
        if len(arr) == 0:
            raise ValueError("Array is empty.")

        print('The given array is', arr)# Display the original array
        sorted_arr = radix_sort(arr.copy())  # Sorting a copy to keep the original array intact
        print('The sorted order is:', sorted_arr) # Display the sorted array

    except ValueError as e:
         # Handle ValueError exceptions (e.g., empty array)
        print(f"Error: {e}")

# Check if the script is being run as the main program
if __name__ == "__main__":
    main()

In the above Code, the counting_sort subroutine is used within the radix_sort algorithm to sort the elements based on their individual digits. The counting_sort subroutine counts the frequence of each digit at specified exponential postion and then sorts the elements based on this information. The radix_sort algorithm iterates through each digit position( units, tens, hundreds etc) to fully sort the array.

Sample Test Cases:

Test Case 1: Input: Enter the elements of the array separated by space: 170 45 75 90 802 24 2 66 Output: The given array is [170, 45, 75, 90, 802, 24, 2, 66] The sorted order is: [2, 24, 45, 66, 75, 90, 170, 802]
Test Case 2: Input: Enter the elements of the array separated by space: 5 4 3 2 1 Output: The given array is [5, 4, 3, 2, 1] The sorted order is: [1, 2, 3, 4, 5]
Edge Case: Input: Enter the elements of the array separated by space: Output: Error: Array is empty.
Error Case: Input: Enter the elements of the array separated by space: 5 3 d 5 6 Output: Error: invalid literal for int() with base 10: 'd'

Code in C++:

/*Copyrights to venkys.io
For more information, visite https://venkys.io"/

C++ program to sort a given array in order using radix sort algorithm. */
// Stable : Yes
// Inplace : No
// Adaptive : No

// Space complexity: O(n+k) where
  // n = number of elements in the input array
  // k = range of input values (number of unique digits)

//Time Complexity: O(d*(n+k)) /O(n+k) in simplified version
  // n=no. of elements
  // k= range of input values
  // d= no. of digits in maximum value

#include<iostream>
// This line includes the input/output stream header file
using namespace std;
// This line declares that elements from the C++ Standard Library (std).
// Specifically, it allows the usage of elements, such as cout and cin, without needing to prefix them with std::

//function to get the maximum value in arr[]
int max(int arr[],int n){
	# Initialize maxele to the first element of the array
    int maxele=arr[0];
    for(int i=0;i<n;i++){
    	# Check if the current element is greater than the current maxele
        if (arr[i]>maxele){
        	 # If yes, update maxele to the current element
            maxele=arr[i];
        }
    }
    # Return the maximum element found in the array
    return maxele;
}
//function to do counting sort of arr[] according to the digit represented by exp.
void countingSort(int arr[],int n,int decimalplace){
	// Initialize an array to store the count of each digit (0 to 9)
    int count[10];
    
	// Initialize an array to store the sorted output
    int output[n];
    // Initialize count array with zeros
    for(int i=0;i<10;i++){
        count[i]=0;
    }
    //processing count array 
    for(int i=0;i<n;i++){
        int index=arr[i]/decimalplace;
        count[index%10]+=1;
    }
    //cumulative count array
    for(int i=1;i<10;i++){
        count[i]+=count[i-1];
    }
    //Build the output array
    for(int i=n-1;i>=0;i--){
        int index=arr[i]/decimalplace;
        output[count[index%10]-1]=arr[i];
        count[index%10]-=1;
    }

		//Cope the output array to arr[]
    for(int i=0;i<n;i++){
        arr[i]=output[i];
    }
}
//Radix Sort
void radixSort(int arr[],int n){
	//Find maximum number to know number of digits
    int m=max(arr,n);
    int decimalplace=1;
    //Do counting sort for every digit. Instead of passing digit directly, exp is passed.
    //exp is 10^i where i is current digit number. This helps in sorting in (one's, ten's and hundred's digit place)
    while(m/decimalplace>0){
        countingSort(arr,n,decimalplace);
        decimalplace*=10;
    }

		//Print the sorted array
    for(int i=0;i<n;i++){
        cout<<arr[i]<<" ";
    }
    cout<<endl;
}

// driver code to test the above two functions: Counting function and radix sort
int main(){

    {
        int n;
        // Prompt the user to enter the number of elements in the array
        cout << "Enter no. of elements in array: ";
        // Check if the input for array size is not an integer or non-positive
        if (!(cin >> n) || n <= 0) {
		// Check if the input for array size is not an integer
        cout << "Error: Please enter a valid integer for the array size." << endl;
        return 1;
        // Return 1 to indicate an error       
		 }
        int arr[n];
        // Prompt the user to enter the elements of the array
        cout << "Enter elements in array: ";
        // Iterate through each element of the array and input values from the user
        for (int i = 0; i < n; i++) {
        	// Check if the input for array elements is not an integer
            if (!(cin >> arr[i])) {
            cout << "Error: Please enter valid integers for array elements." << endl;
            return 1; // Return 1 to indicate an error
            }
        }
        // Call the radixSort function to sort the array
        radixSort(arr, n);
    } 
    return 0;  // Return 0 to indicate successful execution of the program
}

C++ Radix Sort Algorithm Explanation:

The C++ implementation of radix sort follows a similar approach to the Python implementation.

countingSort() function: In C++, the counting sort is defined as a separate function. Like in Python, it iterates through the array, calculates the frequency of digits, and distributes the elements into buckets. After processing all digits, it updates the original array with the sorted elements.
radixSort() function: The radixSort function finds the maximum number in the array and then repeatedly calls the countingSort function for each digit place to sort the numbers in the array.

Sample Test Cases:

Test Case 1: Input: Enter no. of elements in array: 5 Enter elements in array: 12 43 7 9 5

Output: 5 7 9 12 43
Test Case 2: Input: Enter no. of elements in array: 8 Enter elements in array: 109 2 301 42 56 17 208 95

Output: 2 17 42 56 95 109 208 301
Test Case 3: Input: Enter no. of elements in array: -3 Output: Error: Please enter a valid integer for the array size.
Test Case 4: Input: Enter no. of elements in array: 4 Enter elements in array: 5 2 d 8

Output: Error: Please enter valid integers for array elements.
Test Case 5: Input: Enter no. of elements in array: 0 Output: Error: Please enter a valid integer for the array size.

Code in Java:

/* Copyrights to venkys.io */
/* For more programs, visit venkys.io */
/* Java program for Radix sort */

// Stable: Yes
// Inplace: No
// Adaptive: No

// Space complexity: O(n) where n = number of elements in the input array

// Time Complexity: O(d*(n+k)) / O(n+k) in simplified version
// n=no. of elements
// k= range of input values
// d= no. of digits in maximum value

import java.util.InputMismatchException;// Importing InputMismatchException class for handling input errors
import java.util.Scanner; // Importing Scanner class from java.util package for user input

public class RadixSort {

    static int output[]; // Sorted output array

    // Function to sort radixes
    public static void VSDRadix(int n, int[] a, int digits) {
        int k = 0;// Initialize the digit position to the least significant digit
        int temp[] = new int[n]; // Temporary array to hold radixes
        while (k < digits) { // Loop until all digits are processed
            for (int i = 0; i < n; i++) {
                if (k > 0)
                    // Extract the k-th digit using modulo and division
                    temp[i] = (int) ((a[i] / Math.pow(10, k)) % 10);
                else
                    // For the least significant digit, use modulo only
                    temp[i] = a[i] % 10;
            }
            // Perform counting sort based on the current digit
            VSDcountingsort(n, a, temp);
            k++; // Move to the next digit
        }
    }

    // Function to perform counting sort on radixes
    public static void VSDcountingsort(int n, int[] a, int temp[]) {
        int[] count = new int[10];// Create an array to store the count of occurrences of each radix.
        output = new int[n];// Create an array to store the sorted output.

        // Initializing all the elements of counting array to zero
        for (int i = 0; i < count.length; i++)
            count[i] = 0;

        // Storing the count of occurrences of each element from the input array to count array
        for (int i = 0; i < n; i++) {
            count[temp[i]]++;
        }

        // Computing cumulative sum from count array
        for (int i = 1; i < 10; i++) {
            count[i] += count[i - 1];
        }

        // Sorting radixes. Traverse the input array backward. 
        //For each element, use the count array to determine its position in the sorted output array.
        for (int i = n - 1; i >= 0; i--) {
            output[count[temp[i]] - 1] = a[i];
            count[temp[i]]--;//Decrease the count of that radix in the count array.
        }

        // Copy the sorted output array back to the original array.
        for (int i = 0; i < n; i++) {
            a[i] = output[i];
        }
    }

    // Function to count maximum number of digits
    public static int VSDdigitcount(int max) {
        int d = 0;// Initialize the digit count to 0
        while (max > 0) {
            d++; // Increment the digit count for each digit
            max = max / 10; // Remove the last digit by dividing the number by 10
        }
        return d; // Return the final count of digits
    }

    // Function to get maximum element in the array
    public static int VSDMax(int n, int[] a) {
        int max = 0;
        // Iterate through each element in the array
        for (int i = 0; i < n; i++) {
            // Check if the current element is greater than the current max
            if (a[i] > max) {
                // If yes, update max to the current element
                max = a[i];
            }
        }
        // Return the maximum element found in the array
        return max;
    }

    // Function to print the output
    public static void VSDprintOutput(int n, int[] a) {
        System.out.println("The sorted array is:");
        for (int i = 0; i < n; i++)
            System.out.print(a[i] + " ");

        System.out.println();
    }

    public static void main(String args[]) {
        // Create a Scanner object to read user input from the console.
        Scanner scanner = new Scanner(System.in);
        try {
            // Prompt the user to enter the size of the array.
            System.out.print("Enter the size of the array: ");
            // Initialize n to null to validate user input.
            Integer n = null;
             // Continue prompting the user until a valid positive integer is entered for the array size.
            while (n == null || n <= 0) {
                try {
                    // Attempt to read an integer from the user input.
                    n = scanner.nextInt();
                    // Check if the entered size is not positive.
                    if (n <= 0) {
                        System.out.println("Invalid size. Please enter a positive integer.");
                    }
                } catch (InputMismatchException e) {
                    // Handle the case where a non-integer value is entered.
                    System.out.println("Invalid input. Please enter a valid integer.");
                    scanner.nextLine();// Clear the buffer to prevent an infinite loop.
                }
            }

            // Create an array to store the elements of the array.
            int[] a = new int[n];
            
            // Prompt the user to enter the elements of the array.
            System.out.println("Enter the elements of the array:");
            // Iterate through each element of the array and input values from the user.
            for (int i = 0; i < n; i++) {
                // Use a loop to handle invalid input until a valid integer is entered.
                while (true) {
                    if (scanner.hasNextInt()) {
                        // If the entered value is an integer, assign it to the array.
                        a[i] = scanner.nextInt();
                        break; // Exit the loop as a valid integer is obtained.
                    } else {
                        // Display an error message for invalid input and clear the buffer.
                        System.out.println("Invalid input. Please enter valid integers.");
                        scanner.nextLine();// Clear the buffer to avoid an infinite loop.
                    }
                }
            }
            // Find the maximum element in the array
            int max = VSDMax(n, a);
            
            // Count the number of digits in the maximum element.
            int d = VSDdigitcount(max);
            
            // Perform Radix Sort on the array.
            VSDRadix(n, a, d);
            
            // Print the sorted array.
            VSDprintOutput(n, a);
        } finally {
            // Close the scanner to avoid resource leaks.
            if (scanner != null) {
                scanner.close();
            }
        }
    }
}

Java Radix Sort Algorithm Explanation:

Few of the functions used in Java are:

VSDMax→ To obtain maximum element from an array
VSDdigitcount→ To count number of digits in the maximum value
VSDRadix→ To sort numbers based on their radix
VSDcountingsort→Performs counting sort algorithm
VSDprintOutput→ To print the sorted array through radix sort algorithm.

Sample Test Cases:

Test Case 1: Enter the size of the array: 5 Enter the elements of the array: 29 13 55 7 42 The sorted array is: 7 13 29 42 55
Test Case 2 (Edge Case - Empty Array): Enter the size of the array: 0 Invalid size. Please enter a positive integer.
Test Case 3 (Handling Invalid Input - Non-Integer Size): Enter the size of the array: abc Invalid input. Please enter a valid integer. Enter the size of the array: 5 Enter the elements of the array: 1 2 3 4 5 The sorted array is: 1 2 3 4 5
Test Case 4 (Handling Invalid Input - Non-Integer Elements): Enter the size of the array: 4 Enter the elements of the array: 10 a 30 40 Invalid input. Please enter valid integers. 20 10 40 30 The sorted array is: 10 20 30 40