Exploring Array Algorithms: Searching a Sorted Matrix

Array algorithms play a crucial role in computer science and programming, providing versatile solutions for storing and manipulating data. In this blog, we'll delve into the concept of searching a sorted matrix and explore an algorithmic approach to efficiently locate a target element.

Introduction

In Searching a Sorted Matrix, the matrix is sorted in a specific order, either row-wise or column-wise, or even both. The goal is to efficiently find a specific target element within the matrix. Let's consider a scenario where the matrix is sorted in ascending both row-wise and column-wise order. This scenario is often encountered in real-world applications, such as databases and image processing. In this case, binary search can be applied to each row individually.

Problem Statement

Given a sorted matrix, we aim to find a target element efficiently.

Binary Search

Binary search is a divide-and-conquer algorithm that repeatedly divides the search space in half. In the context of a sorted matrix, binary search can be applied both horizontally and vertically, optimizing the search process. In this scenario, we apply binary search in row-wise order.

The binary search algorithm divides the search space in half with each comparison. It is well-suited for sorted arrays and matrices. By applying binary search on both rows and columns simultaneously, we can efficiently locate the target element. The algorithm starts with the entire collection as the initial search space. Calculate the mid-point of the current search space. If there is an odd number of elements, the mid-point is taken as the floor of the division. Compare the value at the mid-point with the target value.

If the mid-point value is equal to the target, the search is successful, and the index of the mid-point is returned. If the target is less than the mid-point value, the search space is restricted to the lower half. If the target is greater, the search space is restricted to the upper half. Repeat the process on the narrowed-down search space until the target is found or the search space becomes empty. If the search space becomes empty, the target is not in the collection.

Searching

Consider a 3x4 matrix where each row is sorted in ascending order:

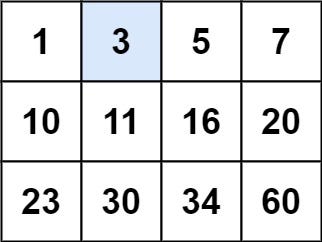
Searching matrix

Let's say we want to find if the number 3 is present in this matrix. A brute-force approach might involve searching each element one by one, but we can leverage the sorted nature of each row to design a more efficient algorithm.

Algorithm

Perform a binary search within the row.
Compare the middle element with the target.
If the middle element is equal to the target, return True.
If the middle element is less than the target, adjust the search space to the right or Update the 'low' index accordingly to 'mid + 1'.
If the middle element is greater than the target, adjust the search space to the left or Update the 'high' index accordingly to 'mid - 1'.

This approach optimally utilizes the sorted nature of each row

Python Code

# Copyrights to venkys.io
# For more programs visit venkys.io 
# Python program for Searching a sorted Matrix

# time complexity:O(m*n)
# space complexity:O(1)

# Define a function named searchMatrix that takes a 2D matrix and a target integer as input
def searchMatrix(matrix, target: int):
    # Get the number of rows in the matrix
    rows = len(matrix)
    # Get the number of columns in the matrix
    cols = len(matrix[0])
    # Calculate the total number of elements in the matrix
    items = rows * cols
    # Initialize low and high for binary search
    low = 0
    high = items - 1
    
    # Perform binary search on the matrix
    while low <= high:
        # Calculate the middle index
        mid = (low + high) // 2
        # Calculate the element at the middle index in the matrix
        temp = matrix[mid // cols][mid % cols]
        
        # Check if the target is equal to the middle element
        if temp == target:
            return True
        # If the target is less than the middle element, update the high index
        elif target < temp:
            high = mid - 1
        # If the target is greater than the middle element, update the low index
        else:
            low = mid + 1
    
    # If the target is not found, return False
    return False

#test drive code:
if __name__ == "__main__":
    # Matrix
    rows, cols = map(int, input().split())

    # Initialize an empty matrix
    matrix = []

    # Input each row of the matrix
    for _ in range(rows):
        row = list(map(int, input().split()))
        matrix.append(row)
    # Target integer
    target = 3
    # Check if the target is found in the matrix using the searchMatrix function
    if searchMatrix(matrix, target):
        print("True")
    else:
        print("False")

The output of the above test case

    3 is found in the matrix

Java Code

// Copyrights to venkys.io
// For more programs visit venkys.io
// Java program for Searching a sorted Matrix

// time complexity:O(m*n)
// space complexity:O(1)

import java.util.*;
public class Main {
    
    // Function to perform binary search on a sorted matrix
    static boolean searchMatrix(int[][] matrix, int target) {
        // Get the number of rows in the matrix
        int rows = matrix.length;
        // Get the number of columns in the matrix
        int cols = matrix[0].length;
        // Calculate the total number of elements in the matrix
        int items = rows * cols;
        // Initialize low and high for binary search
        int low = 0;
        int high = items - 1;

        // Perform binary search on the matrix
        while (low <= high) {
            // Calculate the middle index
            int mid = (low + high) / 2;
            // Calculate the element at the middle index in the matrix
            int temp = matrix[mid / cols][mid % cols];
            
            // Check if the target is equal to the middle element
            if (temp == target) return true;
            // If the target is less than the middle element, update the high index
            else if (target < temp) high = mid - 1;
            // If the target is greater than the middle element, update the low index
            else low = mid + 1;
        }

        // If the target is not found, return false
        return false;
    }

    // Main method
    public static void main(String[] args) {
        // Matrix
        Scanner scanner = new Scanner(System.in);

        // Input the dimensions of the matrix
        int rows = scanner.nextInt();
        int cols = scanner.nextInt();

        // Initialize a 2D array to store the matrix
        int[][] matrix = new int[rows][cols];

        // Input each element of the matrix
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                matrix[i][j] = scanner.nextInt();
            }
        }

        // Target integer
        int target = 3;

        // Check if the target is found in the matrix using the searchMatrix function
        if (searchMatrix(matrix, target)) System.out.println("Found");
        else System.out.println("Not Found");
    }
}

C++ Code

// Copyrights to venkys.io
// For more programs visit venkys.io 
// CPP program for Searching a sorted Matrix

// time complexity:O(m*n)
// space complexity:O(1)

#include<iostream>
#include<vector>

using namespace std;

// Function to perform binary search on a sorted matrix
bool searchMatrix(vector<vector<int>> &matrix, int target) {
    // Get the number of rows in the matrix
    int rows = matrix.size();
    // Get the number of columns in the matrix
    int cols = matrix[0].size();
    // Calculate the total number of elements in the matrix
    int items = rows * cols;
    // Initialize low and high for binary search
    int low = 0;
    int high = items - 1;

    // Perform binary search on the matrix
    while (low <= high) {
        // Calculate the middle index
        int mid = (low + high) / 2;
        // Calculate the element at the middle index in the matrix
        int temp = matrix[mid / cols][mid % cols];

        // Check if the target is equal to the middle element
        if (temp == target) return true;
        // If the target is less than the middle element, update the high index
        else if (target < temp) high = mid - 1;
        // If the target is greater than the middle element, update the low index
        else low = mid + 1;
    }
    // If the target is not found, return false
    return false;
}

// Function to take matrix input from the user
vector<vector<int>> inputMatrix(int rows, int cols) {
    vector<vector<int>> matrix(rows, vector<int>(cols, 0));
    // cout << "Enter the elements of the matrix:" << endl;
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            cin >> matrix[i][j];
        }
    }
    return matrix;
}

// Main method
int main() {
    // Get the number of rows and columns in the matrix from the user
    int rows, cols;
    // cout << "Enter the number of rows in the matrix: ";
    cin >> rows;
    // cout << "Enter the number of columns in the matrix: ";
    cin >> cols;

    // Matrix input
    vector<vector<int>> matrix = inputMatrix(rows, cols);

    // Target input
    int target;
    // cout << "Enter the target integer: ";
    cin >> target;

    // Check if the target is found in the matrix using the searchMatrix function
    if (searchMatrix(matrix, target)) court << "Found";
    else court << "Not Found";

    return 0;
}

Test Cases

Test Case 1: Basic Search

Matrix:
```
1 3 5 7
10 11 16 20
23 30 34 60
```

Target: 3 Expected Output: "3 is found in the matrix" Explanation: This test case involves a simple matrix where the target element (3) exists. The algorithm should correctly identify and output that the target is found in the matrix.

Test Case 2: Target Not Present

Matrix:
```
  1 3 5 7
  10 11 16 20
  23 30 34 60
```
Target: 13 Expected Output: "13 is not found in the matrix" Explanation: In this scenario, the target element (13) is not present in the matrix. The algorithm should correctly output that the target is not found.

Test Case 3: Single Element Matrix

Matrix:
```
  5
```
Target: 5 Expected Output: "5 is found in the matrix" Explanation: This test involves a matrix with a single element. The target is equal to the only element in the matrix. The algorithm should identify and output that the target is found.

Test Case 4: Larger Matrix, Target Present

Matrix:


  2, 4, 6, 8, 10
  12 14 16 18 20
  22 24 26 28 30
  32 34 36 38 40

Target: 22 Expected Output: "22 is found in the matrix" Explanation: This test involves a larger matrix where the target element (22) exists. The algorithm should efficiently identify and output that the target is found.

Test Case 5: Larger Matrix, Target Not Present

Matrix:
```
  
    2 4 6 8 10
    [12 14 16, 18, 20],
    [22, 24, 26, 28, 30],
    [32, 34, 36, 38, 40]
  
```
Target: 25 Expected Output: "25 is not found in the matrix" Explanation: In this scenario, the target element (25) is not present in the matrix. The algorithm should correctly output that the target is not found.

Test Case 6: Empty Matrix

Matrix: [] (Empty matrix) Target: 7 Expected Output: "7 is not found in the matrix" Explanation: This test involves an empty matrix. The algorithm should output that the target is not found as there are no elements in the matrix.

Additional Considerations

Test cases involving edge conditions, such as the smallest possible matrix or the largest possible matrix, to ensure the algorithm handles boundary cases correctly.
Performance testing with larger matrices to evaluate the efficiency of the algorithm.
Test cases with negative numbers, duplicates, or matrices are sorted in descending order to validate the algorithm's flexibility and accuracy.

Running these test cases against the searching algorithm for a sorted matrix will help ensure its correctness and effectiveness in finding target elements within different types of matrices.

Time and Space Complexity Analysis

All three implementations have a time complexity O(log(m*n)), where m and n are the number of rows and columns in the matrix, respectively. The time complexity is logarithmic due to the binary search.
The space complexity is O(1) since the algorithm uses a constant amount of extra space for all three programs Java, C++, and Python.

Real-world Applications

Databases and Information Retrieval:
- Sorted matrices are used to represent and store structured data in databases.
- Search operations in databases often involve finding specific records or values, and a sorted matrix allows for efficient searching.
Geographical Information Systems (GIS):
- GIS applications often organize geographical data in matrices where each cell represents a location.
- Searching for specific geographic features or values, such as elevation or temperature, can be efficiently performed using sorted matrix search algorithms.
Financial Applications:
- Financial data, such as stock prices or currency exchange rates, can be organized in matrices.
- Efficient searching is crucial for tasks like identifying trends, finding specific values, or conducting financial analyses.
Game Development:
- Grid-based games often use matrices to represent game boards or terrain.
- Searching for specific elements or performing pathfinding in games can benefit from an efficient sorted matrix search.
Machine Learning and Data Analytics:
- Matrices are fundamental data structures in machine learning, representing datasets or correlation matrices.
- Searching for specific patterns or features in datasets is a common task in data analytics.
Optimization Problems:
- Matrices are employed in optimization problems where each cell represents a decision variable.
- Searching for optimal solutions or identifying regions of interest in optimization landscapes can be achieved using sorted matrix search.
Image Processing:
- Matrices are commonly used to represent images where each element corresponds to a pixel.
- Searching for specific patterns or features within an image, such as object recognition, can be accelerated using sorted matrix search techniques.