SELECTION SORT
INTRODUCTION OF SELECTION SORT
Selection sort is a simple sorting algorithm that works by repeatedly finding the minimum element from the unsorted portion of a list and swapping it with the first unsorted element. This process continues until the entire list is sorted. Selection sort has a time complexity of O(n^2) and is not suitable for large lists. It is often used for educational purposes to understand the concept of sorting algorithms.
OVERVIEW OF SELECTION SORT
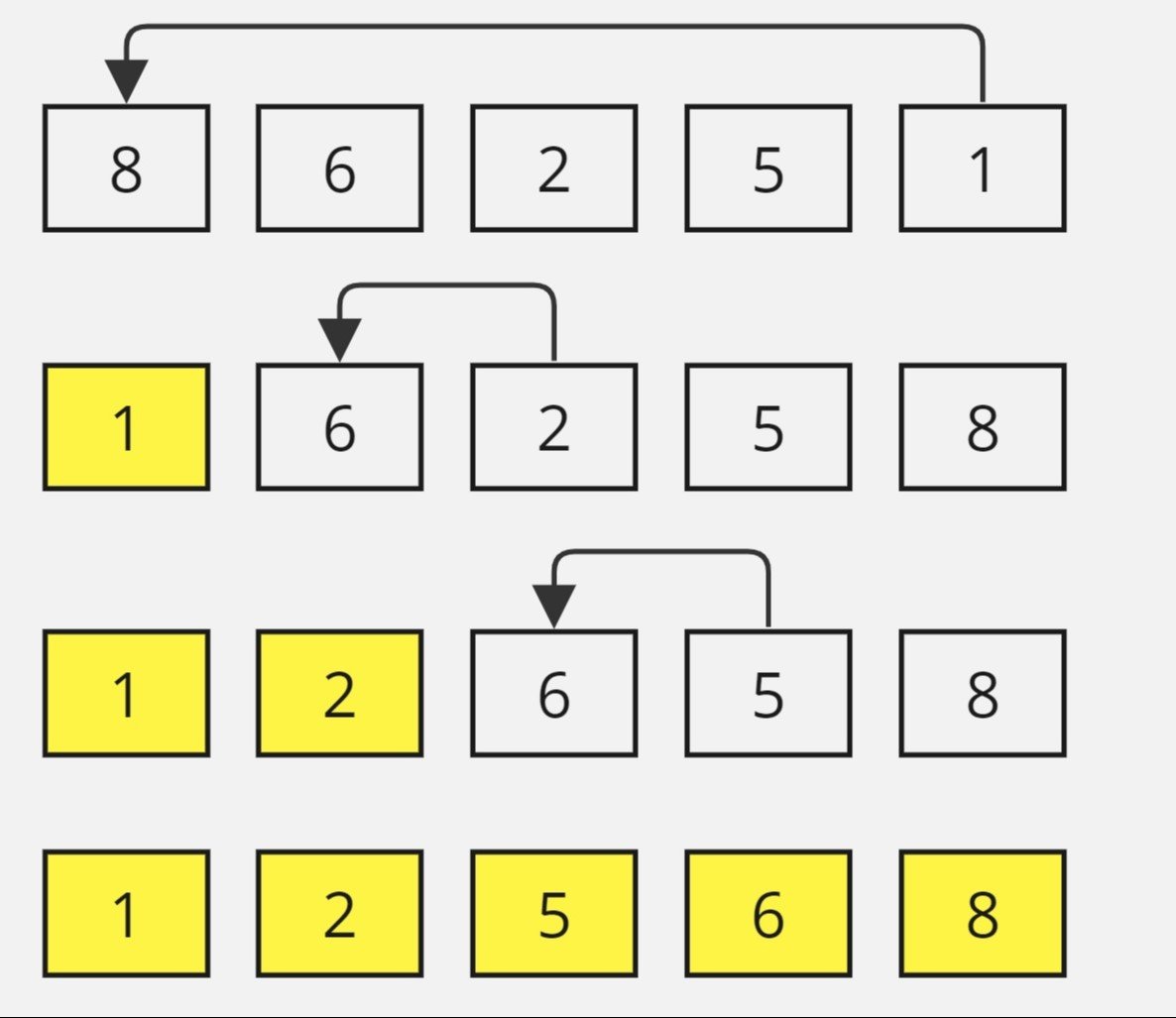
Selection sort begins by considering the entire array as the unsorted region. In each iteration, the algorithm finds the minimum element in the unsorted region and swaps it with the first element of the unsorted region. This effectively expands the sorted region and shrinks the unsorted region. The process is repeated until the entire array is sorted. Although its time complexity is O(n^2), making it less efficient for large datasets, selection sort's simplicity and ease of understanding make it a viable option for small-scale sorting tasks.
Example:
Consider the array [64, 25, 12, 22, 11]. Here's how selection sort would work:
Pass 1:
- Find the smallest element (11) and swap it with the first element:
[11, 25, 12, 22, 64] - Now, the first element is sorted.
Pass 2:
- Find the smallest element among the remaining unsorted elements (12) and swap it with the second element:
[11, 12, 25, 22, 64] - The first two elements are now sorted.
Pass 3:
- Find the smallest element among the remaining unsorted elements (22) and swap it with the third element:
[11, 12, 22, 25, 64]
Pass 4:
- Find the smallest element among the remaining unsorted elements (25) and swap it with the fourth element:
[11, 12, 22, 25, 64]
Pass 5:
- Now, the entire array is sorted:
[11, 12, 22, 25, 64]
CODE
PYTHON
# Copyrights to venkys.io
# For more information, visit venkys.io
# time complexity = O(n^2),
# space complexity = O(1).
def selectionSort(arr):
n = len(arr)
# Traverse through all array elements
for i in range(n):
# Find the minimum element in the unsorted part of the array
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
# Swap the found minimum element with the first element
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Input array from the user
try:
data = list(map(int, input("Enter the elements of the array separated by space: ").split()))
# Call the selectionSort function to sort the array
selectionSort(data)
# Display the sorted array
print('Sorted Array in Ascending Order:')
print(data)
#The error handling is included to handle cases where the user enters non-integer values.
except ValueError:
print("Please enter valid integers for array elements.")
STEP BY STEP EXPLANATION
Below is a step-by-step explanation of the code provided:
- The code begins with the definition of the selection
- Sort function, which takes an array as input and performs the selection sort algorithm on it.
- The selection Sort function starts by getting the length of the array.
- It then iterates through each element of the array using a for loop. The variable 'i' represents the current index of the element being considered in the unsorted portion of the array.
- Inside the outer loop, another loop is used to find the index of the minimum element in the unsorted portion of the array. The variable 'j' represents the index being compared with the current minimum index.
- If the element at index 'j' is found to be smaller than the element at the current minimum index, the minimum index is updated to 'j'.
- After finding the minimum element in the unsorted portion of the array, the code swaps it with the first element of the unsorted portion. This effectively expands the sorted region and shrinks the unsorted region.
- The process of finding the minimum element and swapping it with the first element of the unsorted region continues until the entire array is sorted.
- The main part of the code handles user input and calls the selection Sort function to sort the array.
- It prompts the user to enter the size of the array and then takes input for each element of the array.
- It then calls the selection Sort function, passing the input array as an argument.
- Finally, it displays the sorted array in ascending order by iterating through the elements of the array and printing them.
Please note that the code provided is in different programming languages (Python, Java, and C++), but the logic and steps for the selection sort algorithm remain the same across the languages.
JAVA
// Copyrights to venkys.io
// For more information, visit venkys.io
// time complexity = O(n^2),
// space complexity = O(1).
import java.util.Scanner;
public class SelectionSort {
public static void selectionSort(int[] arr) {
int n = arr.length;
// Traverse through all array elements
for (int i = 0; i < n; i++) {
// Find the minimum element in the unsorted part of the array
int minIdx = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIdx]) {
minIdx = j;
}
}
// Swap the found minimum element with the first element
int temp = arr[i];
arr[i] = arr[minIdx];
arr[minIdx] = temp;
}
}
// Input array from the user
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
try {
System.out.print("Enter the size of the array: ");
int size = scanner.nextInt();
int[] data = new int[size];
for (int i = 0; i < size; i++) {
System.out.print("Enter element " + (i + 1) + ": ");
data[i] = scanner.nextInt();
}
// Call the selectionSort method to sort the array
selectionSort(data);
// Display the sorted array
System.out.println("Sorted Array in Ascending Order:");
for (int element : data) {
System.out.print(element + " ");
}
// The error handling is included to handle cases where the user enters non-integer values.
} catch (java.util.InputMismatchException e) {
System.out.println("Please enter valid integers for array elements.");
}
}
}
STEP BY STEP EXPLANATION
- The code starts by importing the necessary packages and defining the Selection Sort class.
- The selection Sort method is defined, which takes an integer array as input and performs the selection sort algorithm on it. The time complexity of the algorithm is O(n^2), and the space complexity is O(1).
- Inside the selection Sort method, the array length is stored in the variable n.
- The outer loop iterates through each element of the array from index 0 to n-1. This loop represents the sorted part of the array.
- Inside the outer loop, the minimum value is searched for in the unsorted part of the array. The variable min Idx is used to keep track of the index of the minimum value.
- The inner loop starts from index i+1 and iterates through the remaining unsorted elements. If an element smaller than the current minimum is found, the min Idx is updated.
- After finding the minimum value, it is swapped with the first element of the unsorted part. This brings the minimum value to its correct position in the sorted part of the array.
- The sorted array is printed after the outer loop completes. The elements are displayed in ascending order.
- The main method is defined to get input from the user and call the selection Sort method. It starts by creating a Scanner object to read input.
- The user is prompted to enter the size of the array. Then, an array of that size is created.
- The user is prompted to enter each element of the array, and the values are stored in the data array.
- The selection Sort method is called with the data array as an argument to sort the array.
- Finally, the sorted array is displayed to the user.
- Error handling is included to handle cases where the user enters non-integer values.
C++
// Copyrights to venkys.io
// For more information, visit venkys.io
// time complexity = O(n^2),
// space complexity = O(1).
#include <iostream>
#include <vector>
using namespace std;
void selectionSort(vector<int>& arr) {
int n = arr.size();
// Traverse through all array elements
for (int i = 0; i < n; i++) {
// Find the minimum element in the unsorted part of the array
int minIdx = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIdx]) {
minIdx = j;
}
}
// Swap the found minimum element with the first element
swap(arr[i], arr[minIdx]);
}
}
// Input array from the user
int main() {
try {
cout << "Enter the size of the array: ";
int size;
cin >> size;
vector<int> data(size);
for (int i = 0; i < size; i++) {
cout << "Enter element " << (i + 1) << ": ";
cin >> data[i];
}
// Call the selectionSort function to sort the array
selectionSort(data);
// Display the sorted array
cout << "Sorted Array in Ascending Order:" << endl;
for (int element : data) {
cout << element << " ";
}
} catch (const exception& e) {
cout << "Please enter valid integers for array elements." << endl;
}
return 0;
}
STEP BY STEP EXPLANATION
- The Selection Sort class is defined at the beginning of the code along with the import of the required packages.
- The selection Sort method is defined; it applies the selection sort algorithm to an integer array as input. The algorithm has an O(n^2) time complexity and an O(1) space complexity.
- The array length is kept in the variable n within the selection Sort method.
- The array's elements are iterated through from index 0 to n-1 in the outer loop. The sorted portion of the array is represented by this loop.
- The unsorted portion of the array is searched for the minimum value inside the outer loop. The index of the lowest value is tracked using the variable min Idx.
- Iterating through the remaining unsorted elements, the inner loop begins at index i+1. The minIdx is changed if an element is discovered that is smaller than the existing minimum.
- The minimum value is found and then swapped with the unsorted part's first element. This moves the lowest value in the array's sorted portion to its proper location.
- Following the completion of the outer loop, the sorted array is printed. In increasing order, the elements are shown.
- The main method's definition calls the selection Sort function after receiving user input. To read input, a Scanner object must first be created.
- A prompt asking for the array's size is displayed to the user. After that, an array of that size is made.
- Each element of the array is entered by the user, and the values are saved in the data array.
- To sort the array, the selection Sort method is called and the data array is sent as an argument.
- The user is finally presented with the sorted array.
- To manage situations when the user submits non-integer values, error handling is included.
TEST CASES
EXAMPLE 1:
Input :
Enter the elements of the array separated by space:
Output :
Sorted Array in Ascending Order: []
Explanation :
The selection sort algorithm should handle edge cases such as an empty array. Since there are no elements to sort, the output should be an empty array.
EXAMPLE 2 :
Input :
Enter the elements of the array separated by space: 4 2 7 1 9
Output :
Sorted Array in Ascending Order:
[1, 2, 4, 7, 9]
Explanation :
The selection sort algorithm selects the minimum element in each iteration and swaps it with the first unsorted element. After the first iteration, the smallest element (1) is in its correct position. This process repeats until the array is sorted.
EXAMPLE 3:
Input :
Enter the elements of the array separated by space: 5 2 8 2 5
Output :
Sorted Array in Ascending Order:
[2, 2, 5, 5, 8]
Explanation :
Selection sort handles arrays with duplicate values. The algorithm selects the minimum element, and in case of duplicates, it preserves their relative order.
TIME AND SPACE COMPLEXITY
The time complexity of the Selection Sort algorithm is O(n^2), where 'n' is the number of elements in the array. This is because, in the worst-case scenario, for each element in the array, it needs to traverse the entire remaining unsorted portion of the array to find the minimum element and then perform a swap.
The space complexity of the Selection Sort algorithm is O(1) This is because the algorithm only requires a constant amount of extra space to store variables like loop counters, indices, and temporary variables for swapping elements. The space required does not depend on the size of the input array, making it an "in-place" sorting algorithm.
REAL-WORLD APPLICATION FOR SELECTION SORT
Selection sort, despite its inefficiency for large datasets, can still be useful in certain scenarios. One common real-world application is in situations where memory usage is a concern. Since selection sort only requires a constant amount of additional memory, it can be advantageous in environments with limited resources.
Another application of selection sort is in sorting small lists or arrays where simplicity and ease of implementation are more important than efficiency. For example, selection sort can be used in sorting a deck of cards or a small list of names.
Overall, while selection sort may not be the most efficient sorting algorithm for large-scale tasks, it still has practical applications in specific contexts where simplicity and limited memory usage are prioritized.
