Shell Sort
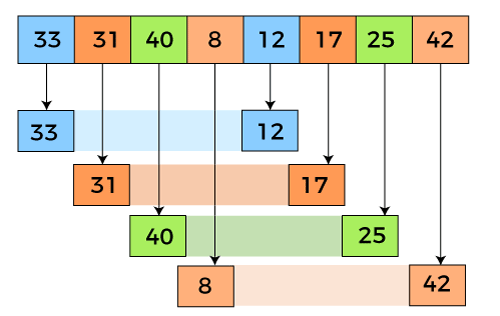
Introduction to Shell Sort:
The Shell Sort algorithm is a simple and efficient sorting algorithm that is used to sort an array of elements. It is a divide-and-conquer algorithm, which means that it divides the original array into smaller sub-arrays, sorts each sub-array separately, and then combines the sorted sub-arrays back into a single sorted array.
The algorithm works by dividing the input array into two halves, then dividing each half into smaller sub-arrays and sorting each sub-array using any sorting algorithm of your choice. The sorted sub-arrays are then merged back into a single sorted array. This process continues, and the size of the sub-arrays is decreased at each iteration until the entire array is sorted.
The key element in the Shell Sort algorithm is the interval, which represents the range of elements that are compared and sorted at each iteration. The interval is determined based on the gap size, which is the initial distance between elements in the sorted sub-array. The gap size is decreased by a certain factor at each iteration, allowing the algorithm to efficiently sort the array.
The Shell Sort algorithm is relatively simple and easy to understand. However, it is not the most efficient sorting algorithm, particularly for large arrays.
What is a Comparision based and an In-place comparison based Sort?
Comparison-based sorting algorithms rely on comparing elements of an array to determine their order. They work by repeatedly iterating through the array and swapping adjacent elements that have the wrong order. There are several comparison-based sorting algorithms, some of the most common ones include : Bubble sort, Quicksort, Mergesort, Selection sort, Insertion sort and Radix Sort
In-place comparison based sorting, on the other hand, is a type of sorting algorithm that does not use additional memory to sort the array. In contrast with in-place comparison based sorting, sorting algorithms like Radix sort may use additional memory to sort the array.
In-place comparison-based sorting algorithms are generally not as efficient as non-comparison-based sorting algorithms, such as counting sort or radix sort. This is because comparison-based algorithms, even when in-place, may require additional memory for temporary variables during the sorting process and need to perform multiple swaps. However, in-place comparison-based sorting algorithms are still commonly used, especially for small arrays or when additional memory is constrained.
Interval and knuth formula in shell sort
Interval is the range of elements to be sorted at each iteration of the Shell Sort algorithm. It determines the number of elements that will be considered in each iteration and how much progress will be made in each step.
Knuth Formula, on the other hand, is an approach to determine the shell size at each iteration. It is a formula that helps to determine the smallest gap size for a given array. In the Shell Sort algorithm, the gap size is used to divide the array into halves, and to discover the correct gap size is the key to the algorithm.
The knuth formula is:
Explain
gap_size = n/2
for j = 0 to log_n(k) - 1
gap_size = gap_size/k
k = 2
size = size of the array
Understanding Shell Sort through an Example:
Consider an array with input elements array[]={8, 12, 4, 25, 9, 6, 2, 20}
First we need to initally use a large gap and then repeatedly reduce the gap until it become 1.
The final pass in sorting is done by implementing insertion sort algorithm.
In the above example the array has 8 elements.
So initial gap(h) is n/2 and then n/4 and then n/8 and so on.
Step by Step Internal Execution:
Initial array: {8, 12, 4 25, 9, 6, 2, 20}
- First Pass(h= n/2=4)
- Compare elements that are h position apart and then swap them if necessary
- {8, 12, 4 25, 9, 6, 2, 20} here 8 and 9 are compared. Since they are in order there is no swapping
- {8, 12, 4 25, 9, 6, 2, 20}: 12 and 6 are compared and swapped
- {8, 12, 4 25, 9, 6, 2, 20}: 4 and 2 are compared and swapped
- {8, 12, 4 25, 9, 6, 2, 20}: 25 and 20 are compared and swapped.
- After swapping the array would be {8, 6, 2, 20, 9, 12, 4, 25}
- Second Pass(h=n/4=2)
- Compare elements that are h position apart and then swap them if necessary.
- {8, 6, 2, 20, 9, 12, 4, 25}
- Compare 8 and 2 and swap them. The array would be {2, 6, 8, 20, 9, 12, 4, 25}
- Compare 6 and 20 next. No swapping required.
- Compare and swap 8 and 9. No swapping required.
- Compare and swap 20 and 12. The array would be {2, 6, 8, 12, 9, 20, 4, 25}
- Compare and swap 9 and 4 followed by 20 and 25.
- The Resulting array would be {2, 6, 8, 12, 4, 20, 9, 25}
- Third Pass (h=n/8=1)
- Since the gap is one. Compare all the adjacent elements.
- Perform insertion sort on entire array with a gap 1.
- After this step the array is fully sorted :{ 2, 4, 6, 8, 9, 12, 20, 25}
- Final Sorted Array : { 2, 4, 6, 8, 9, 12, 20, 25}
Advantages of Shell Sort:
- Adaptability:
- Shell Sort is adaptive, meaning its performance is influenced by the initial order of the elements. It tends to perform better on partially sorted or nearly sorted datasets compared to algorithms with a fixed gap.
- In-Place Sorting:
- Shell Sort is an in-place sorting algorithm, meaning it doesn't require additional memory space for auxiliary data structures. It sorts the elements within the array itself, making it memory-efficient.
- Ease of Implementation:
- The algorithm is relatively easy to implement, making it accessible for educational purposes and scenarios where a simple sorting algorithm is sufficient.
- Efficiency for Small Datasets:
- Shell Sort can be efficient for small to moderately sized datasets. Its complexity is generally better than simple algorithms like Bubble Sort or Insertion Sort, especially in scenarios where the dataset is not too large.
- Time Complexity Improvements:
- By using diminishing increment sequences (gap sizes), Shell Sort addresses some of the inefficiencies of simple sorting algorithms. It introduces a form of optimization that helps reduce the number of comparisons and swaps.
- No Extra Memory Overhead:
- Unlike some other advanced sorting algorithms, Shell Sort doesn't require additional memory overhead for recursive calls or complex data structures.
- Balanced Trade-Offs:
- Shell Sort provides a balanced trade-off between simplicity and efficiency. It's more efficient than some basic sorting algorithms while maintaining a level of simplicity that makes it suitable for educational purposes and small-scale applications.
- Variability in Gap Sequences:
- The flexibility to choose different gap sequences allows some customization based on the characteristics of the data being sorted. This adaptability can be an advantage in certain scenarios.
While Shell Sort has these advantages, it's important to note that for very large datasets or datasets with specific patterns, more advanced sorting algorithms like QuickSort or MergeSort might be preferred for optimal performance. The choice of sorting algorithm depends on the specific requirements and characteristics of the data being sorted.
Disadvantages of Shell Sort:
- It is not the most efficient sorting algorithm, particularly for large arrays, as it has a time complexity of O(n⁰) where n is the number of elements in the input array, which is not as efficient as other algorithms like merge sort which has a time complexity of O(n log n).
- It is not suitable for sorting arrays with irregularly spaced values, like dates or names.
- It is not very stable, meaning that elements with the same value may be rearranged during sorting, unlike other sorting algorithms like merge sort which is a stable sorting algorithm.
- It is not an algorithm for large datasets. It is not well-suited for large datasets, as it has a time complexity of O(n⁰) which is significant compared to other algorithms like merge sort or quick sort, which have a time complexity of O(n log n) or O(n log n), respectively.
- It can be difficult to optimize for large datasets and may require a lot of memory to store large data sets.
Real Scenarios of Shell Sort:
The Shell sort algorithm can be used in a range of real-world applications, including:
- GUI sorting - It can be used to sort display items in a graphical user interface (GUI) like a desktop file explorer or an image gallery, to make it easier for the user to find the item they are looking for.
- Text sorting - It can be used to sort lines of text, such as in a word processor or a code editor, which can be useful for sorting code files or sorting zip files.
- Sorting line cards - It can be used to sort 2D line cards, such as those found in a card reader for swiping messages.
- Sorting strings of text - It can be used to sort strings of text, such as names or addresses, to make it easier to sort the data in a spreadsheet or a database.
- Sorting array of integers - It can be used to sort an array of integers, for example, sort the account balance of a customer in a database of customer information.
- Sorting the database of company information - It can be used to sort information of companies like their products, services etc.
- Sorting strings of characters - It can be used to sort strings of characters, such as passwords, to make it easier to manage a password book.
- Shell sort is used in Linux Kernel because it does not use a call stack.( A call stack is a specialized data structure that stores information about active subroutines or functions in a program. )
- Shell sort is used in bzip2 compressor to avoid problems that could come when sorting algorithms exceed a language’s recursion depth.
Optimizing Shell Sort:
There are several ways to optimize the Shell sort algorithm:
- Reduce the number of iterations - One of the most common ways to optimize Shell sort is to reduce the number of iterations. This can be done by choosing a smaller initial shell size or by incrementing the shell size more slowly. The smaller the shell size, the fewer iterations it will take to sort the array.
- Use a more efficient algorithm for smaller subarrays - Another way to optimize Shell sort is to use a more efficient algorithm for smaller subarrays, such as insertion sort or bubble sort. These algorithms have a time complexity of O(n) and are particularly efficient for small arrays.
- Parallelize the sorting process - Shell sort can be parallelized, meaning that multiple elements can be sorted at the same time. by dividing the array into multiple chunks and sorting them simultaneously using multiple processors or threads.
- Use a hybrid approach - Shell sort can be combined with other sorting algorithms, such as quicksort or mergesort, to create a hybrid sorting algorithm. In this approach, Shell sort is used to sort small, irregularly spaced arrays and other sorting algorithm to sort larger, regularly spaced arrays.
- Implement a more efficient data structure - A more efficient data structure, such as a heap or a priority queue, can also help to optimize the Shell sort algorithm. These data structures allow for more efficient comparison and manipulation of elements, which can lead to faster sorting times.
- Optimize the memory usage - The memory usage of the shell sort can be sized according to the size of the input array to optimize the computation.
Time and Space complexity
The time complexity of the provided VSDShellSort algorithm is O(n log n) on average, and O(n^2) in the worst case, where n is the length of the input array.
In the worst case, when the shell size is not chosen appropriately, the algorithm would repeatedly compare the first element of the unsorted sub-array with all other elements in the sub-array until it finds the correct position, resulting in O(n^2) worst-case time complexity.
The space complexity of the VSDShellSort algorithm is O(1) because it sorts the input array in-place, using only a constant amount of additional space.
Python code for Shell Sort:
'''Copyrights to venkys.io
For more information, visite https://venkys.io"/
Python program to sort a given array in order using Shell sort algorithm.'''
# Stable : No
# Inplace : Yes
# Adaptive : Yes
# Space complexity: O(1)
#Time Complexity:O(n^2) in the worst-case scenario, and O(n log n) in the average case scenario.
def VSDShellSort(arr,n):
shellsize=8 # Initialize the initial gap size for Shell Sort
while(shellsize>=1):# Continue the loop until the gap size becomes 1
i=shellsize
k=0
while(i<n and k<shellsize): # Iterate through the array with the current gap size
key=arr[i] # Store the current element as the key
j=i-shellsize # Start comparing with the element 'shellsize' positions before the current element
while j>=0:
if(arr[j]>key):
arr[j+shellsize]=arr[j] # Shift elements greater than the key to the right
else:
break
j-=shellsize
arr[j+shellsize]=key # Insert the key at its correct position in the sorted sequence
if(i+shellsize)>=n:
k+=1
i=k+shellsize # Move to the next group of elements for comparison
else:
i+=shellsize
shellsize=shellsize//2 # Reduce the gap size by half in each iteration
print(*arr,sep=" ") # Print the sorted array
def main():
try:
# Input the number of elements
n = int(input("Enter the number of elements: "))
# Check if the entered number of elements is not a positive integer
if n <= 0:
raise ValueError("Number of elements should be a positive integer.")
# Input the elements of the array and convert them to integers
arr = list(map(int, input("Enter the elements separated by space: ").split()))
# Check if the number of elements entered matches the specified count
if len(arr) != n:
raise ValueError("Number of elements entered doesn't match the specified count.")
# Call the VSDShellSort function to sort the array
VSDShellSort(arr, n)
except ValueError as e:
# Handle the case where an error occurs (e.g., non-integer input)
print(f"Error: {e}")
# Check if the script is executed as the main program
if __name__ == "__main__":
main()
Note: The choice of gap sequence affects its adaptability, and in this case, it uses a fixed gap sequence (shellsize=8 and then halves the gap in each iteration).
- We initialize an shell size with a value (shellsize=8)
- We run a while loop while the value of shellsize is greater than 1. This loop iterates n times. while(shellsize>=1):
- initialize two variables i and k, starting at their initial values. i=shellsize k=0
- Run another while loop while i is less than n and k is less than shellsize. while(i<n and k<shellsize):
- Initialize a variable key and assign the value at the current position in the array to it. key=arr[i]
- We run another while loop while j is greater than or equal to 0. This loop iterates (n - i) times. while j>=0:
- We check if the value at position j in the array is greater than the key. if(arr[j]>key):
- If it is, we assign the value at position j + shellsize to the variable next_j. next_j=arr[j+shellsize]
- We then align the value at position (j + next_j) to position j using another while loop, which iterates (shellsize - 1) times. while(next_j>=j+1): arr[j]=next_j-1 next_j=j+shellsize j+=shellsize
- Once we have iterated the while loop, we exit the inner while loop by using the break statement. This happens if the value at position j is not greater than the key.
- Finally, we assign the value at position j + shellsize to the variable key and increment the value of j. arr[j+shellsize]=key j+=1
- If the value of i is equal to n, we increment the value of k and set the value of i to k + shellsize. if(i+shellsize)>=n
Sample Test Cases:
- Valid Input Case: Enter the number of elements: 5 Enter the elements separated by space: 12 4 6 8 1 1 4 6 8 12
- Invalid Number of Elements Case: Enter the number of elements: -3 Error: Number of elements should be a positive integer.
- Mismatched Element Count Case: Enter the number of elements: 4 Enter the elements separated by space: 2 4 6 Error: Number of elements entered doesn't match the specified count.
- Non-Integer Element Case: Enter the number of elements: 3 Enter the elements separated by space: 7 a 2 Error: invalid literal for int() with base 10: 'a'
C++ code for Shell Sort:
/*Copyrights to venkys.io
For more information, visit https://venkys.io"/
C++ program to sort a given array in order using Shell sort algorithm. */
// Stable: No
// Inplace: Yes
// Adaptive: Yes
// Space complexity: O(1) - sorts in place
// Time Complexity: O(n^2) in the worst-case scenario, and O(n log n) in the average case scenario.
#include<iostream>
#include<vector> // Container to hold elements
#include<string> // String representation for input
#include<sstream> // To convert string input into integer
using namespace std; // Namespace identifies the code as part of the standard library
// Function to perform Shell Sort on the given array
void shellSort(int arr[], int n) {
int shellsize = 8;
// Iterate through decreasing gap sizes until the gap is 1
while (shellsize >= 1) {
for (int i = shellsize, k = 0; i < n && k < shellsize;) {
int key = arr[i];
int j = i - shellsize;
// Compare and shift elements to make room for the key
for (; j >= 0; j -= shellsize) {
if (arr[j] > key) {
arr[j + shellsize] = arr[j];
} else {
break;
}
}
// Insert the key at the correct position in the sorted sequence
arr[j + shellsize] = key;
// Update indices for the next iteration
if (i + shellsize >= n) {
k += 1;
i = k + shellsize;
} else {
i += shellsize;
}
}
// Reduce the gap size for the next iteration
shellsize = shellsize / 2;
}
// Print the sorted array
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
string input;
// Prompt the user to enter the elements separated by space
cout << "Enter the elements separated by space: ";
// Read the entire line of input
getline(cin, input);
// If the input is empty, print an error message and exit
if (input.empty()) {
cout << "Error: Empty input. Please provide elements to sort." << endl;
return 1; // Return 1 to indicate an error
}
// Parse the input string and convert it into an array of integers
stringstream ss(input);
vector<int> elements;
int num;
// Continue parsing until the end of the stringstream
while (ss >> num) {
elements.push_back(num);
}
// If the parsed elements vector is empty, print an error message and exit
if (elements.empty()) {
cout << "Error: No valid integers found in the input. Please provide valid elements." << endl;
return 1; // Return 1 to indicate an error
}
int n = elements.size();
// If the array size is less than or equal to 0, print an error message and exit
if (n <= 0) {
cout << "Error: Invalid array size. Please enter a positive integer for the array size." << endl;
return 1; // Return 1 to indicate an error
}
int arr[n];
// Copy elements from the vector to the array
for (int i = 0; i < n; i++) {
arr[i] = elements[i];
}
// Call the shellSort function to sort the array
shellSort(arr, n);
return 0; // Return 0 to indicate successful execution of the program
}
- The provided Shell Sort implementation is not guaranteed to be stable. Stability in sorting algorithms means that the relative order of equal elements is preserved, and Shell Sort does not explicitly handle this requirement.
- The
shellSortfunction implements the Shell Sort algorithm. It starts with a gap size of 8 and iteratively reduces the gap until it becomes 1. - The outer loop controls the gap size, and the inner loops perform insertion sort within each subset defined by the current gap.
- The sorted array is printed after the sorting process.
Java code for Shell sort:
/* Copyrights to venkys.io */
/* For more programs, visit venkys.io */
/* Java program for Shell sort */
// Stable: No
// Inplace: Yes
// Adaptive: Yes
// Space complexity: O(1)
// Time Complexity: O(n^2) in the worst-case scenario, and O(n log n) in the average case scenario.
import java.util.Scanner; // Importing Scanner class from java.util package for user input
public class ShellSort {
static int n; // Size of the array
static int[] arr; // Array of numbers to be sorted
// Function to perform shell sort
public static void shellSort() {
int shellSize = 8; // Initial shell size
// Continue the sorting process until the shell size becomes 0
while (shellSize >= 1) {
// Iterate through the array with the current shell size
for (int i = shellSize, k = 0; i < n && k < shellSize;) {
int key = arr[i];// Store the current element to be inserted
int j = i - shellSize;
// Move elements greater than key to the right until a smaller or equal element is found,
// or until the beginning of the subarray is reached.
for (; j >= 0; j -= shellSize) {
if (arr[j] > key) {
arr[j + shellSize] = arr[j];// Shift the current element to the right
} else {
break; // Stop shifting if a smaller or equal element is found
}
}
arr[j + shellSize] = key;// Insert the stored element at its correct position
// Move to the next position in the array considering the shell size
if (i + shellSize >= n) {
k += 1;
i = k + shellSize;
} else {
i += shellSize;
}
}
// Reduce the shell size for the next iteration
shellSize = shellSize / 2;
}
}
// Function to print output
public static void printOutput() {
System.out.println("The sorted order is:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String args[]) {
// Create a Scanner object to read user input from the console.
Scanner scanner = new Scanner(System.in);
try {
// Input the elements separated by space
System.out.print("Enter the elements separated by space: ");
// Read the entire line as input.
String input = scanner.nextLine();
// Check for null or empty input
if (input == null || input.trim().isEmpty()) {
System.out.println("Error: Empty input. Please enter valid elements.");
return; // Exit the program to handle the error.
}
// Split the input string into an array of string elements based on space.
String[] elements = input.split(" ");
n = elements.length;// Set the size of the array based on the number of elements.
arr = new int[n];// Initialize the array to store the parsed integers.
// Parse input elements to integers
for (int i = 0; i < n; i++) {
try {
// Parse each element as an integer and assign it to the array.
arr[i] = Integer.parseInt(elements[i]);
} catch (NumberFormatException e) {
// Handle the case where an element is not a valid integer.
System.out.println("Error: Invalid input. Please enter valid integers.");
return;// Exit the program to handle the error.
}
}
// Call the shellSort function to perform the sorting.
shellSort();
// Call the printOutput function to display the sorted array.
printOutput();
} finally {
// Close the scanner to avoid resource leaks
if (scanner != null) {
scanner.close();
}
}
}
}
- The
VSDSortfunction implements the Shell Sort algorithm in Java. It starts with a gap size of 8 and iteratively reduces the gap until it becomes 1. - The outer loop controls the gap size, and the inner loops perform insertion sort within each subset defined by the current gap.
- The sorted array is printed after the sorting process using the
VSDprintOutputfunction.
Sample Test Case 1: Enter the elements separated by space: 5 2 9 1 5 6 The sorted order is: 1 2 5 5 6 9
Sample Test Case 2: Enter the elements separated by space: 10 5 3 8 2 7 9 The sorted order is: 2 3 5 7 8 9 10
Sample Test Case 3 (Empty Input): Enter the elements separated by space: Error: Empty input. Please enter valid elements.
Sample Test Case 4 (Invalid Input - Non-Integer Element): Enter the elements separated by space: 1 2 3 a 5 Error: Invalid input. Please enter valid integers.
Sample Test Case 5 (Invalid Input - Empty Element): Enter the elements separated by space: 1 2 3 5 Error: Invalid input. Please enter valid integers.
