WORD BREAK PROBLEM
WORDBREAK PROBLEM
The Word Break Problem is a common problem in computer science and natural language processing. It involves determining if a given string can be segmented into a space-separated sequence of valid words from a dictionary.
INTRODUCTION OF THE WORD BREAK PROBLEM
The Word Break Problem is a classic dynamic programming problem in computer science. It involves determining whether a given string can be segmented into a space-separated sequence of one or more words, using a given dictionary of words. In other words, the problem is about breaking a string into valid words from a predefined set of words.
OVERVIEW OF THE WORD BREAK PROBLEM
To solve the Word Break Problem, dynamic programming techniques are commonly employed. The idea is to break down the problem into smaller subproblems and use the solutions of those subproblems to build the solution for the original problem. By efficiently storing and reusing the computed results, dynamic programming algorithms can provide an optimal solution.
Here are the key points of the problem:
Input:
- A string s.
- A dictionary of words wordDict.
Output:
- True if s can be segmented into words from wordDict, False otherwise.
example:
Input:
- s = "applepie"
- wordDict =
["apple", "pie", "pen", "pineapple"]
Output:
True
Explanation:
There are two valid ways to segment "applepie" into words from the dictionary:
- "apple pie" - Both "apple" and "pie" are present in the dictionary.
- "applepie" - Both "app" and "lepie" are not present in the dictionary, but "applepie" itself is present as a single word in the dictionary.
Therefore, the output is True since at least one valid segmentation exists.
CODE
PYTHON
# Copyrights to venkys.io
# For more information, visit venkys.io
# Time Complexity: O(2^n).
# The space complexity: O(n).
def wordBreak(user_string, user_words):
# Create a list to store whether the substring up to index i can be segmented
d = [False] * len(user_string)
for i in range(len(user_string)):
for w in user_words:
# Check if the current substring is equal to a word and the preceding substring is breakable
if w == user_string[i - len(w) + 1:i + 1] and (d[i - len(w)] or i - len(w) == -1):
# Mark the current substring as breakable
d[i] = True
return d[-1]
if __name__ == "__main__":
# Get user input for the string
user_string = input()
# Get user input for the list of words
user_words = input().split()
# Check if the string can be segmented using the provided words
result = wordBreak(user_string, user_words)
# Display the result
if result:
print("true")
else:
print("false")
Step-by-Step Explanation of the Code
- the wordBreak function which takes two parameters: user_string and user_words.
- Inside the wordBreak function, a list d is created to store whether the substring up to index i can be segmented.
- The code then iterates through each index of the user_string using a for loop.
- For each index, another loop is used to iterate through each word in the user_words.
- The code checks if the current substring is equal to a word and if the preceding substring is breakable.
- If both conditions are met, the current substring is marked as breakable by setting the corresponding element in d to True.
- Finally, the function returns the last element of d, which indicates whether the entire string can be segmented using the provided words.
- Outside the wordBreak function, the code checks if the script is being run directly and prompts the user to enter a string and a list of words.
- The wordBreak function is called with the user-provided string and words, and the result is stored in the result variable.
- The code then prints the result, indicating whether the true or false .
This code implements a dynamic programming approach to solve the word break problem, which determines whether a given string can be segmented into words from a provided list.
JAVA
/* Copyrights to venkys.io
For more information, visit - venky.io
Time Complexity: O(2^n).
The space complexity: O(n). */
import java.util.ArrayList;
import java.util.HashSet;
import java.util.Scanner;
public class WordBreak {
static boolean wordBreak(String s, ArrayList<String> words) {
// Create a HashSet for faster word lookup
HashSet<String> set = new HashSet<>(words);
// Dynamic programming array to store if substring up to index i can be segmented
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true; // Empty string is always breakable
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
// Check if the current substring is equal to a word and the preceding substring is breakable
if (dp[j] && set.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Get user input for the string
// System.out.print("Enter a string: ");
String userString = scanner.nextLine();
// Get user input for the list of words
// System.out.print("Enter a list of words separated by spaces: ");
String[] userWordsArray = scanner.nextLine().split(" ");
ArrayList<String> userWords = new ArrayList<>();
for (String word : userWordsArray) {
userWords.add(word);
}
// Check if the string can be segmented using the provided words
if (wordBreak(userString, userWords)) {
System.out.println("true");
} else {
System.out.println("false");
}
}
}
Step-by-Step Explanation of the Code
- Import required libraries: The code begins by importing the necessary libraries, including ArrayList, HashSet, and Scanner.
- Define the wordBreak function: This function takes a string s and an ArrayList of words as parameters. It checks whether the string s can be segmented into words from the provided list. The function returns a boolean value indicating whether the string can be segmented.
- Create a HashSet for faster word lookup: A HashSet named set is created to store the words from the provided list. This allows for efficient word lookup during the segmentation process.
- Initialize the dynamic programming array: An array dp of boolean values is initialized to store whether a substring up to index i can be segmented. The array is initialized with false values, except for dp[0] which is set to true to indicate that the empty string is always breakable.
- Perform dynamic programming: Two nested loops are used to iterate through the string s. The outer loop iterates from 1 to the length of s, representing the end index of the current substring. The inner loop iterates from 0 to the current index, representing the start index of the current substring.
- Check if the current substring is breakable: For each substring, the code checks if the preceding substring is breakable (dp[j] is true) and if the current substring is a word present in the HashSet set. If both conditions are met, the dp[i] value is set to true and the loop breaks.
- Return the result: Finally, the function returns the value of dp[s.length()], which represents whether the entire string s can be segmented into words.
- Implement the main function: The main function is responsible for getting user input and calling the wordBreak function. It prompts the user to enter a string and a list of words separated by spaces. It then converts the user input into an ArrayList and passes it to the wordBreak function.
- Print the result: Based on the return value of the wordBreak function, either "TRUE" or "FALSE" is printed to indicate whether the string can be segmented or not.
C++
// Copyrights to venkys.io
// For more information, visit venkys.io
// time Complexity : O(2^n).
// The space complexity: O(n)..
#include <iostream>
#include <vector>
#include <unordered_set>
#include <sstream>
using namespace std;
bool wordBreak(const string& s, const vector<string>& words) {
unordered_set<string> wordSet(words.begin(), words.end());
// Dynamic programming array to store if substring up to index i can be segmented
vector<bool> dp(s.length() + 1, false);
dp[0] = true; // Empty string is always breakable
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
// Check if the current substring is equal to a word and the preceding substring is breakable
if (dp[j] && wordSet.count(s.substr(j, i - j))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
// Get user input for the string
int main() {
string userString;
// cout << "Enter a string: ";
getline(cin, userString);
// Get user input for the list of words
// cout << "Enter a list of words separated by spaces: ";
string word;
vector<string> userWords;
getline(cin, word);
stringstream ss(word);
while (ss >> word) {
userWords.push_back(word);
}
// Check if the string can be segmented using the provided words
if (wordBreak(userString, userWords)) {
cout << "true" << endl;
} else {
cout << "false" << endl;
}
return 0;
}
Step-by-Step Explanation of the Code
- The code begins with the necessary includes for input/output operations, vectors, unordered sets, and string manipulation.
- The wordBreak function takes in a string s and a vector of strings words as parameters. It returns a boolean value indicating whether the string s can be broken into words from the words vector.
- Inside the wordBreak function, an unordered set called wordSet is created from the words vector. This set will be used to quickly check if a word is present in the words vector.
- A vector of booleans called dp is created with a size of s.length() + 1. This vector will be used for dynamic programming to store the breakability of substrings of s.
- The first element of the dp vector is set to true because an empty string is always breakable.
- Two nested loops are used to iterate through all possible substrings of s. The outer loop iterates over the lengths of the substrings, and the inner loop iterates over the starting positions of the substrings.
- For each substring s.substr(j, i - j), the code checks if the substring is present in the wordSet and if the substring starting from position j is breakable (i.e., dp[j] is true).
- If both conditions are satisfied, the dp value for the current position i is set to true and the inner loop is exited.
- After the loops, the final value of dp[s.length()] represents whether the entire string s can be broken into words from the words vector.
- In the main function, the user is prompted to enter a string and a list of words separated by spaces.
- The input string and words are stored in variables userString and userWords, respectively.
- The wordBreak function is called with userString and userWords as arguments, and the result is printed as "TRUE" or "FALSE" accordingly.
- The program ends with a return statement.
Time Cases :
EXAMPLE 1 :
Input :
Enter a string: applepenapple
Enter a list of words separated by spaces: apple pen
Output :
true
Explanation:
The string "applepenapple" can be segmented into "apple", "pen", and "apple," all of which are present in the dictionary.
EXAMPLE 2 :
Input :
Enter a string : “ “
Enter a list of words separated by spaces: word break test
Output :
true
Explanation:
EXAMPLE 3 :
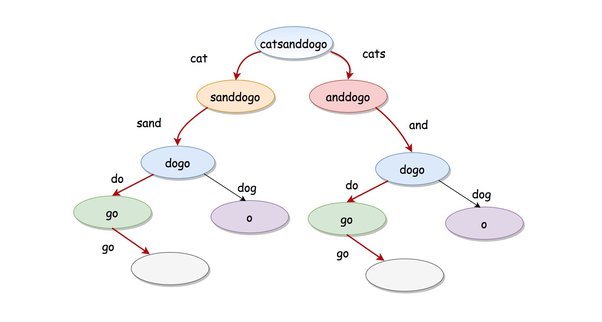
Input :
Enter a string: catsandog
Enter a list of words separated by spaces: cats", "dog", "sand", "and", "cat
Output :
False
Explanation:
It's not possible to break the string "catsandog" into valid words from the dictionary.
TIME AND SPACE COMPLEXITY
The time and space complexity of the provided code for the Word Break Problem can be analyzed as follows:
- Time Complexity: The code consists of two nested loops. The outer loop iterates through the characters of the input string, and the inner loop iterates through the words in the provided word list. Therefore, the time complexity can be approximated as
O(n * m),where n is the length of the input string and m is the number of words in the word list. - Space Complexity: The code uses a boolean list d to store the intermediate results of whether substrings can be segmented into words. The size of the d list is equal to the length of the input string. Therefore, the space complexity is
O(n),where n is the length of the input string.
REAL-WORLD APPLICATION FOR WORDBREAK PROBLEM
The Word Break Problem has several real-world applications in computer science and natural language processing. Here are a few examples:
- Spell Checking: In text editors or word processors, the Word Break Problem can be used to check the spelling of words by breaking the input text into individual words and comparing them against a dictionary of valid words. This helps identify and correct spelling mistakes.
- Search Engines: Search engines use the Word Break Problem to process user queries and match them with relevant documents. By breaking down the query into individual words and matching them against indexed words, search engines can retrieve accurate search results.
- Sentiment Analysis: The Word Break Problem is used in sentiment analysis tasks, where the goal is to determine the sentiment or emotion associated with a given text. By breaking down the text into words and analyzing the sentiment of each word, sentiment analysis models can classify the overall sentiment of the text.
- Machine Translation: In machine translation systems, the Word Break Problem is crucial for breaking down sentences in the source language into individual words and then translating them into the target language. This helps maintain the correct word order and structure during the translation process.
- Text Segmentation: Text segmentation is an important task in natural language processing, where the goal is to divide a given text into meaningful segments, such as sentences or paragraphs. The Word Break Problem can be used to segment the text by breaking it into individual words and then grouping them based on punctuation or other criteria.
